2 Introdução ao R

R é uma linguagem de programação de alto nível voltada para visualização e análise de dados. Em essência foi inspirada na linguagem de programação S (do inglês stats). Foi inicialmente escrita por Ross Ihaka e Robert Gentleman no departamento de estatística da universidade de Auckland na Nova Zelândia. Atualmente a linguagem é mantida pelo grupo R Core Team composto por pessoas do mundo inteiro que tentam melhorar a linguagem dia após dia. Esse conteúdo foi baseado no livro THE R BOOK escrito por Crawley (2012), sendo considerado a bíblia do R.

O kernel do R e os pacotes podem ser baixados pelo CRAN - Comprehensive R Archive Network. Abaixo é apresentada a sintaxe para instalar pacotes em R:

  # Via CRAN
  install.packages("nome_do_pacote")
  
  # Via github (Pacote remotes)
  remotes::install_github("nome_do_repositorio/nome_do_pacote")

O objetivo deste capítulo é abordar conceitos básicos do R. Caso existam informações que você acha relevante estar aqui, sinta-se à vontade para contribuir.

2.1 Definição de variáveis

Para atribuir um valor à uma variável usamos o símbolo <- ou =. No caso da seta, o símbolo deve apontar no sentido da variável e não do valor. Segundo Wickham and Grolemund (2017), é uma boa prática de programação utilizar a seta <- ao invés do =. A seguir é apresentado um trecho de código de como pode ser realizada a declaração e atribuição de valores na linguagem R:

  a <- "Olá!"
  b <- 42
  22 -> c

2.1.1 Tipos primitivos

Agora que sabemos atribuir valores a uma variável, vamos falar sobre os tipos primitivos do R. Segundo a hierarquia do R, todo valor numérico é uma instância da classe pai: numeric. Basicamente, o tipo double (classe filha de numeric) é atribuído à todo número declarado sem sufixo. No entanto, ao se definir um sufixo, outras tipagens podem ser atribuídas às variáveis. Como por exemplo, o tipo integer: através da adição do sufixo L ao valor da variável e o tipo complex: através do sufixo i. Outros tipos primitivos são: os valores booleanos TRUE e FALSE(instâncias da classe logical) e os caracteres (instâncias da classe character)

Exemplo de declaração dos tipos primitivos

  # Inteiro
  a <- 7L
  
  # Double
  b = 14.01
  
  # Booleano
  k <- FALSE
  
  # Complexo
  g <- 12i 
  
  # Caractere
  couse <- 'cool'
  
  # Para inspecionar o valor das variáveis
  b

## [1] 14.01

  # Para verificar a classe
  class(a)

## [1] "integer"

  # Para ver o tipo
  typeof(b)

## [1] "double"

  # Para removê-las
  rm(a)

Se quiser saber mais sobre o tipo complex, consulte a subseção Para saber mais.

2.1.2 Tipos de dados estruturados

Agora que conhecemos os tipos primitivos, vamos aprender sobre vetores e matrizes. Apenas relembrando, podemos dizer que vetores são estruturas unidimensionais que seguem um sentido, contendo 1 linha e N colunas ou 1 coluna e N linhas. Por outro lado, a matriz é um vetor com N-dimensões sendo sua representação básica um vetor bidimensional composto por linhas e colunas. Na Figura 2.1 é apresentado um exemplo das estruturas mencionadas.

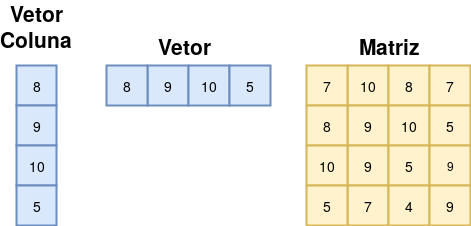
Figure 2.1: Estrutura de dados: Vetor e Matriz

No R há dois tipos de vetores:

Vetores atômicos: Compostos por qualquer tipo primitivo e também do tipo chamado raw.
Listas: São vetores recursivos que podem ser compostos por outras listas.

Colocando de maneira simples, vetores atômicos são homogêneos, ou seja, apenas aceitam um tipo. Se alocado mais de um tipo no vetor, é convertido pelo tipo mais forte. A hierarquia de tipos no R é apresentada na Figura 2.2.

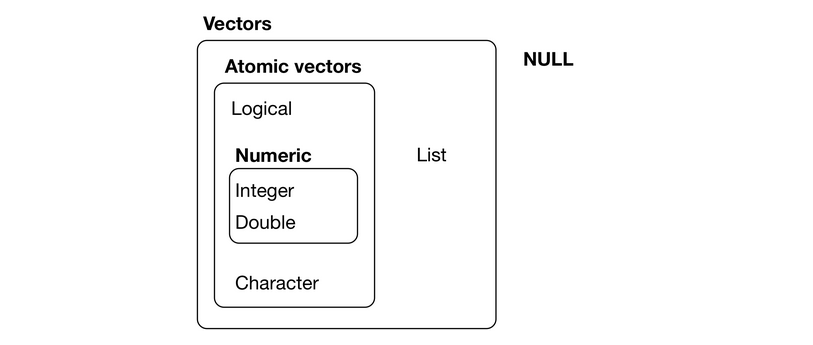
Hierarquia de dados - Fonte: @hadley2017

Figure 2.2: Hierarquia de dados - Fonte: Wickham and Grolemund (2017)

A Figura 2.2 deve ser interpretada de baixo para cima. Seguindo esta ordem:

character
complex
numeric
double
logical

Para declarar um vetor em R usa-se c(), desta forma:

  # Vetor lógico
  vetor_boleano <- c(FALSE, TRUE, TRUE, FALSE)
  
  # Vetor númerico
  vetor_numerico <- c(3.14, 6.28, 2.3)
  
  # Vetor de caractere
  vetor_char <- c("ola", "pessoal", "!")

A conversão de tipos é apresentada na célula abaixo:

  # Esse é um vetor misturado
  vetor_misturado <- c("teste", FALSE, 21)

  # Visualização dos valores atribuídos
  vetor_misturado

## [1] "teste" "FALSE" "21"

Então, segundo a ideia de hierarquia de tipos do R, o vetor da célula acima será convertido para o tipo charactere continuará sendo atômico 🥁.

  # Para verificar se é atômico
  is.atomic(vetor_misturado)

## [1] TRUE

Por outro lado, as listas aceitam diversos tipos, sendo organizadas em listas de listas, por isso, são chamadas de vetores recursivos. Podemos implementar uma lista através do comando list(), deste modo:

  # Lista de boleanos
  lista_boleano <- list(FALSE, TRUE, TRUE, FALSE)
  
  # Lista de inteiros
  lista_inteiro <- list(12L, 10L, 7L)

Podemos criar uma lista de diversos tipos, da seguinte maneira:

  # Lista com todos os tipos 
  lista_misturada <- list(FALSE, 12L, 't', 2i)

  # Visualização da lista
  lista_misturada

## [[1]]
## [1] FALSE
## 
## [[2]]
## [1] 12
## 
## [[3]]
## [1] "t"
## 
## [[4]]
## [1] 0+2i

Para verificar se a lista é atômica utiliza-se o comando is.atomic(). Abaixo é apresentado a utilização do comando no vetor criado anteriormente:

  # Séra ela atômica?
  is.atomic(lista_misturada)

## [1] FALSE

A seguir é apresentado um exemplo com uma lista não atômica, ou seja, uma lista heterogênea composta de vários tipos. Mas, será ela uma lista mesmo ? 🧛🏿‍♂️

  # Verificar se é uma lista
  is.list(lista_boleano)

## [1] TRUE

Podemos checar o tamanhos dos nossos vetores usando a função length().

Já sabemos dos tipos de vetores, agora vamos para as matrizes. As matrizes seguem a mesma ideia dos vetores atômicos. Podemos implementá-la usando o comando matrix(), deste modo:

  library(knitr)

  # Minha matriz com números inteiros com caractere
   matriz <- matrix(data = c(1:25, rep("teste", 5)), nrow = 5, ncol=6)
   
   # Para visualizar a matriz
   knitr::kable(matriz)

1	6	11	16	21	teste
2	7	12	17	22	teste
3	8	13	18	23	teste
4	9	14	19	24	teste
5	10	15	20	25	teste

Então, de acordo com a hierarquia de tipos, a nossa matriz será convertida para character. Podemos verificar seu tipo, desta forma:

  # Para verificar se é matriz
  is.matrix(matriz)

## [1] TRUE

  # Para consultarmos por index
  matriz[1,4]

## [1] "16"

Podemos acessar os valores através dos índices de linha e coluna matriz[linha, coluna].

2.1.3 Data Frame

Um Data Frame pode ser entendido como uma matriz (Figura 2.1) composta por linhas e colunas, cujas colunas representam as variáveis (atributos) e as linhas representam observações. A Figura 2.3 apresenta um Data frame onde é possível observar as definições mencionadas anteriormente. A partir da imagem podemos inferir que o aluno José obteve 7 na disciplina de Álgebra Linear.

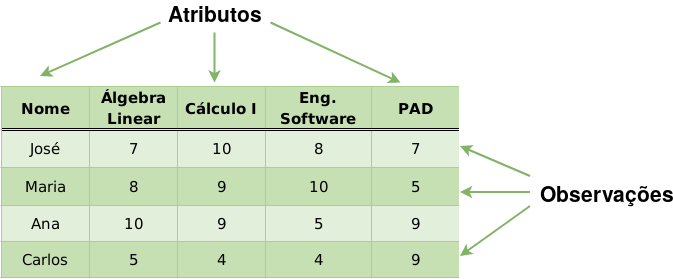
Representação de um Data frame - Fonte: @gk4gk2019

Figure 2.3: Representação de um Data frame - Fonte: GeeksforGeeks (2018)

O trecho de código a seguir apresenta a implementação do Data frame apresentado na Figura 2.3.

  # Importação do pacote 
  library(tibble)  
  
  # Criação do tibble
  df_escola <- tibble::tibble(Aluno = c("José", "Maria", "Ana", "Carlos"),
                              `Álgebra Linear` = c(7, 10, 8, 7),
                              `Cálculo I` = c(8, 9, 10, 5),
                              `Eng. Software` = c(10, 9, 5, 9),
                              `PAD` = c(5, 7, 4, 9))
    
  # Visualização dos dados 
  df_escola

## # A tibble: 4 x 5
##   Aluno  `Álgebra Linear` `Cálculo I` `Eng. Software`   PAD
##   <chr>             <dbl>       <dbl>           <dbl> <dbl>
## 1 José                  7           8              10     5
## 2 Maria                10           9               9     7
## 3 Ana                   8          10               5     4
## 4 Carlos                7           5               9     9

Neste minicurso, vamos usar o pacote tibble no lugar do método data.frame contido no base do R. Dado que o tibble possui diversas vantagens em relação ao tradicional data.frame. Por exemplo, no tibble criado anteriormente é possível observar os tipos de cada atributo. Como o pacote tibble não faz a conversão de atributos do tipo character para factor de forma automática, a etapa de análise de dados se torna mais simples.

Agora que sabemos a definição de um Data frame, vamos ler um conjunto de dados em .csv e observar algumas características:

  # Importação do pacote readr
  library(readr)
  
  # Lendo nosso conjunto de dados
  iris <- readr::read_csv(file = "./data/iris.csv",)

  # Verificando a classe dos nossos dados
  class(iris)

## [1] "spec_tbl_df" "tbl_df"      "tbl"         "data.frame"

  # Verificando o tipo dos nossos dados
  typeof(iris)

## [1] "list"

Podemos usar quaisquer dos métodos apresentados anteriormente para manipular e obter informações do data.frame no tibble. O código acima mostra que o tibble criado possui três classes: tbl_df, tbl e data.frame. É possível observar que o tibble possui como classe comum o data.frame.

Podemos tirar algumas conclusões, a primeira é que, existe uma classe chamada data.frame do tipo list. A segunda é que, a lista em R é heterogênea, portanto, nosso Data frame pode conter vários tipos. Para verificar se a classe data.frame é atômica, retomamos a função is.atomic():

  # Verificando se é atomico nosso df
  is.atomic(iris)

## [1] FALSE

Podemos acessar os atributos de um Data Frame de diversos modos, sendo um deles, utilizando o símbolo $:

  # Para verificar as primeiras linhas
  head(iris$Species)

## [1] "setosa" "setosa" "setosa" "setosa" "setosa" "setosa"

Vamos criar mais Data Frame para fixar o aprendizado:

   # Criação do Data Frame
   data_frame <- tibble::tibble(
     Risco=c(FALSE,FALSE, FALSE, FALSE,TRUE),              
     Animal=c("Cachorro", "Gato", "Capivara", "Girafa", "Leão"),
     Periculosidade=c(200, 400, 0, 7, 1000))
  
  # Podemos acessar os valores individuais usando o '$'
  data_frame$Animal

## [1] "Cachorro" "Gato"     "Capivara" "Girafa"   "Leão"

Risco	Animal	Periculosidade
FALSE	Cachorro	200
FALSE	Gato	400
FALSE	Capivara	0

2.2 Operações Básicas

Agora que sabemos como declarar uma variável, um vetor e Data frame(s), nesta subseção vamos dar algumas dicas e falar sobre alguns métodos estatísticos.

2.2.1 Dicas úteis

Para importar os pacotes no R usa-se o comando library(). Caso esteja com dúvida sobre uma determinada função, use o comando ?nome_do_pacote::nome_da_funcao.

  # Para importar um pacote
  library(kohonen)

  # Documentação da função som do pacote kohonen
  ?kohonen::som

Para especificar o diretório de trabalho, usamos o comando setwd() e para verificar o diretório atual getwd().

  # Para verificar seu diretório atual
  getwd() 
  
  # Para definir um novo diretório
  setwd("/home/felipe/R")

2.2.2 Estatística básica

Nesta seção, vamos focar em como aplicar as estatísticas básicas. Não iremos definir formalmente cada uma das funções estatísticas abordadas, para mais informações consulte (http://cursos.leg.ufpr.br/ecr/). Nos exemplos a seguir iremos aplicar as seguintes funções estatísticas:

Medidas de posição
- Média
- Mediana
Medidas de dispersão
- Desvio padrão

Para verificar o desvio padrão do conjunto, podemos utilizar a função sd() do pacote stats (incluso por padrão no R). Podemos verificar a média com mean() que é uma função do pacote base (incluso por padrão no R) e a mediana com median() do pacote stats.

Como demonstração, vamos utilizar o conjunto de dados do filme Star Wars:

  # Vamos usar o dado do filme Star Wars do pacote dplyr*
  suppressMessages(library(dplyr))
  starwars <- dplyr::starwars
  
  # Vamos visualizar o dado
  dplyr::glimpse(starwars)

## Observations: 87
## Variables: 13
## $ name       <chr> "Luke Skywalker", "C-3PO", "R2-D2", "Darth Vader", "Leia O…
## $ height     <int> 172, 167, 96, 202, 150, 178, 165, 97, 183, 182, 188, 180, …
## $ mass       <dbl> 77.0, 75.0, 32.0, 136.0, 49.0, 120.0, 75.0, 32.0, 84.0, 77…
## $ hair_color <chr> "blond", NA, NA, "none", "brown", "brown, grey", "brown", …
## $ skin_color <chr> "fair", "gold", "white, blue", "white", "light", "light", …
## $ eye_color  <chr> "blue", "yellow", "red", "yellow", "brown", "blue", "blue"…
## $ birth_year <dbl> 19.0, 112.0, 33.0, 41.9, 19.0, 52.0, 47.0, NA, 24.0, 57.0,…
## $ gender     <chr> "male", NA, NA, "male", "female", "male", "female", NA, "m…
## $ homeworld  <chr> "Tatooine", "Tatooine", "Naboo", "Tatooine", "Alderaan", "…
## $ species    <chr> "Human", "Droid", "Droid", "Human", "Human", "Human", "Hum…
## $ films      <list> [<"Revenge of the Sith", "Return of the Jedi", "The Empir…
## $ vehicles   <list> [<"Snowspeeder", "Imperial Speeder Bike">, <>, <>, <>, "I…
## $ starships  <list> [<"X-wing", "Imperial shuttle">, <>, <>, "TIE Advanced x1…

  # Vamos ver a média de ano de nascimento
  mean(starwars$birth_year)

## [1] NA

  # Observe que o NA gera um erro na nossa média, vamos removê-lo
  mean(starwars$birth_year, na.rm = TRUE)

## [1] 87.56512

  # Mediana
  median(starwars$birth_year, na.rm = TRUE)

## [1] 52

  # Podemos procurar pela menor data de nascimento
  min(starwars$birth_year, na.rm = TRUE)

## [1] 8

  # Pelo máximo também
  max(starwars$birth_year, na.rm = TRUE)

## [1] 896

  # Desvio padrão 
  sd(starwars$birth_year, na.rm = TRUE)

## [1] 154.6914

2.3 Estruturas de decisão

No R, os IF's da vida - “se chover e fizer frio, não vou à praia” possuem uma estrutura semelhante ao Java. A seguir, são apresentados exemplos das estruturas de decisão do R com o uso do conjunto de dados star wars.

  personagem <- "BB8"  

  if(personagem %in% starwars$name){
    "Tem o personagem BB8 nos dados"
  } else if("Padmé" %in% starwars$name) {
    "Tem a personagem Padmé nos dados"
  } else {
    "Não possui esse personagem"
  }

## [1] "Tem o personagem BB8 nos dados"

2.4 Iteração

Em R para iterar sobre objetos como lists ou vectors utiliza-se o comando de reptição for. A sintaxe para utilizar o comando for no R é semelhante ao comando em Python. Na célula abaixo é apresentado um exemplo de foreach “para cada elemento da estrutura faça” na linguagem R:

  # Foreach
  for(i in head(starwars$name, 3)){
    print(i)
  }

## [1] "Luke Skywalker"
## [1] "C-3PO"
## [1] "R2-D2"

2.5 Manipulação de dados

Vamos utilizar o pacote dplyr do kit de ferramentas Tidyverse para manipular os valores de um data.frame. Para isso, criamos o seguinte data.frame:

meu_df <- tibble::tibble(
    aluno_id = c(1, 2, 3, 4, 5, 6),
    aluno_sexo = c("Masculino", "Feminino","Masculino", "Feminino", "Masculino", "Feminino"),
    aluno_curso = c("História", "História", "Matemática",
                    "Estatística", "Matemática", "Estatística"),
    aluno_media = c(2.1, 3.5, 4.0, 1.0, NA, 4.9),
    aluno_avaliacao = c("Ruim", "Ruim", "Excelente",
                        "Ruim", "Nenhum", "Excelente"))

aluno_id	aluno_sexo	aluno_curso	aluno_media	aluno_avaliacao
1	Masculino	História	2.1	Ruim
2	Feminino	História	3.5	Ruim
3	Masculino	Matemática	4.0	Excelente
4	Feminino	Estatística	1.0	Ruim
5	Masculino	Matemática	NA	Nenhum
6	Feminino	Estatística	4.9	Excelente

A seguir são descritos os método do pacote dplyr utilizados nos exemplos:

select - Seleção de atributos de um Data Frame;
filter - Filtro de observações de acordo com uma lógica pré-definida;
mutate - Criação de novos atributos;
group_by - Criação de grupos para aplicação de funções de agregação;
summarize - Função de agregação aplicada em grupos.

Com base nos métodos acima, vamos manipular nosso Data Frame ?

  # Importação do pacote dplyr
  library(dplyr)
  
  # Filtro pelo atributo "aluno_avaliano"
  filtro <- dplyr::filter(meu_df, meu_df$aluno_avaliacao == "Ruim")
 
  # Seleção dos atributos "aluno_curso", "aluno_avaliacao" e "aluno_media"
  selecao <- dplyr::select(filtro, aluno_curso, aluno_avaliacao, aluno_media)
  
  # Criação de um grupo de cursos
  grupo <- dplyr::group_by(selecao, aluno_curso)
 
  # Agregação pela média de cada curso
  media <- dplyr::summarize(grupo, media_grupo = mean(aluno_media))

aluno_curso	media_grupo
Estatística	1.0
História	2.8

No exemplo acima foram realizadas algumas operações sobre o data.frame. Sobre o resultado da filtragem foi feita a seleção dos atributos aluno_curso, aluno_avaliacao e aluno_media. A partir da seleção dos atributos agrupamos os dados segundo o atributo aluno_curso. E por fim, calculamos a média do atributo aluno_media revelando o curso e a média dos alunos que obtiveram uma avaliação ruim 🐻. Mas, o código ficou muito grande, como podemos melhorar? Substituindo por apenas uma variável, desta forma:

  # Filtro pelo atributo "aluno_avaliano"
  meu_df1 <- dplyr::filter(meu_df, meu_df$aluno_avaliacao =="Ruim")

  # Seleção dos atributos "aluno_curso", "aluno_avaliacao" e "aluno_media"
  meu_df1 <- dplyr::select(meu_df1, aluno_curso, aluno_avaliacao, aluno_media)
  
  # Criação de um grupo de cursos
  meu_df1 <- dplyr::group_by(meu_df1, aluno_curso)
 
  # Agregação pela média de cada curso
  meu_df1 <- dplyr::summarize(meu_df1, media_grupo = mean(aluno_media))

aluno_curso	media_grupo
Estatística	1.0
História	2.8

Melhorou um pouco, não? Mas podemos melhorar ainda mais utilizando o símbolo %>%. O %>% é chamado de pipe ela é permite com que a resposta da primeira atribuição seja utilizada como primeiro parâmetro da função seguinte, desta forma:

meu_vetor <- c(1, 3, 5, 7, 9) %>% mean()
  
meu_vetor

## [1] 5

A partir disto não precisamos usar a variável meu_vetor como parâmetro da função mean(). Mas e se eu quiser adicionar mais parâmetros? Opa, você pode e deve! Isso segue a mesma linha de raciocínio da função, desta forma:

meu_vetor <- c(2, 4, 6, 8, NA) %>% mean(na.rm=TRUE)

meu_vetor

## [1] 5

Agora, vamos otimizar nossa manipulação usando pipe da seguinte maneira:

  # exemplo de uso do operador pipe
  df <- meu_df %>% filter(aluno_avaliacao == "Ruim") %>%
    select(aluno_curso, aluno_avaliacao, aluno_media) %>%
    group_by(aluno_curso) %>%
    summarize(media_grupo = mean(aluno_media))

aluno_curso	media_grupo
Estatística	1.0
História	2.8

Essa é a principal função do operador pipe, tornar o código mais limpo e reprodutível.

2.6 Exemplos

Para encerrarmos esse capítulo de R, vamos mostrar uma análise de dados aplicada no mundo real. Para isso, iremos utilizar dois conjuntos de dados obtidos através da plataforma kaggle. Os conjuntos de dados correspondentes a série temporal de mudança climática da temperatura da superfície terrestre terrestre e os continentes de cada país. O objetivo da análise é verificar qual continente registrou a maior média anual de temperatura.

  # Importação dos pacotes utilizados
  library(readr)     # Leitura de dados retangulares
  library(dplyr)     # Métodos para manipulação de dados
  library(lubridate) # Métodos para trabalhar com dados do tipo date 
  
  # Leitura dos dados de mudança climática
  temperature_countries <-
  readr::read_csv("./data/GlobalLandTemperaturesByCountry.csv")

  # Leitura e seleção dos dados de continentes
  continent <- 
    readr::read_csv("./data/countryContinent.csv") %>%
    dplyr::select(country, continent) # Seleção do atributo continente

  # Filtro a partir do ano 2000 e extração da média anual (talvez não seja a melhor abordagem)
  year_temperature <- temperature_countries %>%
    dplyr::filter(dt > "2000-01-01")  %>% # Filtro a partir do ano 2000
    dplyr::mutate(dt = lubridate::year(dt)) %>% # Transformando pro tipo date
    dplyr::group_by(Country, dt) %>% # Criando um grupo de países
    dplyr::summarise(year_mean = mean(AverageTemperature)) # Agregação pela média
  
  # Junção dos continentes com cada país  
  final_dataset <- year_temperature %>% 
    dplyr::rename(country = Country) %>% # Alterando o nome do atributo
    dplyr::left_join(continent, by="country") %>% # Junção dos dois conjuntos
    dplyr::filter(!is.na(continent)) # Remoção dos valores NA 
  
  # Visualização dos dados
  head(final_dataset, 5)

## # A tibble: 5 x 4
## # Groups:   country [1]
##   country        dt year_mean continent
##   <chr>       <dbl>     <dbl> <chr>    
## 1 Afghanistan  2000      16.7 Asia     
## 2 Afghanistan  2001      15.8 Asia     
## 3 Afghanistan  2002      15.5 Asia     
## 4 Afghanistan  2003      14.9 Asia     
## 5 Afghanistan  2004      15.8 Asia

Agora vamos responder a nossa pergunta: qual o continente que registrou a maior temperatura anual?

  # Criação de um grupo de continentes e agregando pela maior temperatura
  final_dataset %>%
  dplyr::group_by(continent) %>% # Grupo de continentes
  summarise(maior_temp = max(year_mean, na.rm = TRUE)) # Agregação pela temp max

## # A tibble: 5 x 2
##   continent maior_temp
##   <chr>          <dbl>
## 1 Africa          30.3
## 2 Americas        29.0
## 3 Asia            29.7
## 4 Europe          20.3
## 5 Oceania         27.9

A partir desta análise inicial, podemos gerar outras perguntas, por exemplo, qual o ano com a maior média de temperatura registrada ?

  # Criação de um grupo de anos e agregação pelo valor da temperatura, por fim ordenação pelos valores de temperatura
  final_dataset %>%
  dplyr::group_by(dt) %>% # Grupo dos anos 
  dplyr::summarise(maior_temp = max(year_mean, na.rm = TRUE)) %>% # Agregação pelo max
  dplyr::arrange(desc(maior_temp)) %>% # Ordenação pela temperatura
  head(5)

## # A tibble: 5 x 2
##      dt maior_temp
##   <dbl>      <dbl>
## 1  2000       30.3
## 2  2010       30.1
## 3  2012       29.9
## 4  2009       29.9
## 5  2011       29.8

Enfim, podemos responder diversas perguntas com poucas linhas de código. Esperamos que este capítulo tenha despertado sua curiosidade sobre análise de dados. Os materiais base utilizados para criação deste capítulo se encontram nesta subseção.

2.7 Para saber mais

Este foi só o começo! Para continuar e aprender mais, consulte: