2 Regressão

Todas as pessoas pelo menos uma vez na vida já sentiu ou sentirá a necessidade de prever algum acontecimento futuro. Estamos a todo momento assimilando informações para realizar alguma tomada de decisão, seja de forma intrínseca ou não. No contexto de Machine Learning (ML) isso é feito pelas técnicas de regressão. A regressão é uma ferramenta que busca modelar relações entre variáveis dependentes e independentes através de métodos estatísticos (Soto 2013).

Uma variável independente, normalmente representada pela letra \(x\), caracteriza uma grandeza que está sendo manipulada durante um experimento e que não sofre influência de outras variáveis. Já a variável dependente, normalmente representada pela letra \(y\), caracteriza valores que estão diretamente associados à variável independente, ou seja, de forma direta ou indireta \(x\) excerce influência sobre \(y\). Na Figura 2.1 é apresentada a relação entre a expectativa de vida baseada e um índice de felicidade calculado em diversos países obtidos a partir de um levantamento feito por Helliwell et al. (2020). A variável independente nesse exemplo é representada pelo índice de felicidade e a expectativa de vida age como variável independente, dessa forma pode ser observada uma tendência de expectativa de vida maior em países com alto índice de felicidade, com uma força de correlação de 0,77.

Figure 2.1: Relação entre o índice de felicidade e expectativa de vida. Fonte: (Helliwell et al. 2020)

As relações entre as variáveis dependentes e independentes são feitas através de algum coeficiente de correlação. Uma das métricas de correlação mais utilizadas é o coeficiente de Pearson, que mede a associação linear entre duas variáveis (Kirch 2008). Esse coeficiente de correlação pode ser definido pela Equação (2.1), onde \(n\) é o total de amostras, \(\overline{x}\) e \(\overline{y}\) são as médias aritméticas de ambas as variáveis. Os valores do coeficiente de Pearson variam entre -1 e 1, de tal forma que quanto mais próximos desses extremos, melhor correlacionado estão as variáveis. A Figura 2.2 mostra alguns exemplos com gráficos de dispersão de variáveis com diferentes correlações.

\[\begin{equation} r_{xy} = \frac{{}\sum_{i=1}^{n} (x_i - \overline{x})(y_i - \overline{y})} {\sqrt{\sum_{i=1}^{n} (x_i - \overline{x})^2(y_i - \overline{y})^2}} \tag{2.1} \end{equation}\]

Figure 2.2: Diferentes correlações entre variáveis. Fonte: (Helliwell et al. 2020)

Os métodos de regressão se utilizam dessas correlações entre as variáveis para estimar valores não existentes na amostra ou conjunto de dados. Entretanto, nem sempre essas correlações são tão explícitas assim, sendo necessário outras abordagens mais robustas para realizar as previsões. Em ML os modelos de regressão podem ser criados a partir de diversas abordagens, desde as mais simples com poucas configurações de parâmetros e de fácil interpretação do funcionamento, até as abordagens mais complexas. Os métodos de regressão abordados neste capítulo serão Regressão linear, Máquina de vetores de suporte e Árvores de decisão.

2.1 Regressão Linear

A regressão linear é um dos métodos mais intuitivos e utilizados para essa finalidade. Esses métodos são divididos em dois grupos, a regressão linear simples (RLS) e regressão linear múltipla (RLM). A RLS tem como objetivo estabelecer uma relação entre duas variáveis através de uma função, que pode ser definida por:

\[\begin{equation} y_{i} = \alpha+\beta x_{i} \tag{2.2} \end{equation}\]

Onde \(y_{i}\) é a variável alvo, \(\alpha\) e \(\beta x_{i}\) são coeficientes calculados pela regressão, que representam o intercepto no eixo \(y\) e inclinação da reta, respectivamente.

A RLM é semelhante semelhante à RLS, porém possui múltiplas variáveis preditoras, e pode ser definida por:

\[\begin{equation} y_{i} = \alpha+\beta x_{i1}+\beta x_{i2}+...+\beta x_{in} \tag{2.3} \end{equation}\]

Onde \(y_{i}\) é a variável alvo, \(\alpha\) continua sendo o coeficiente de intercepto e \(\beta x_{ip}\) o é coeficiente angular da \(p\)-ésima variável. Ambos os métodos podem ainda serem somados a um termo \(\epsilon\) de erro.

2.1.1 Coeficientes da regressão linear

Existem diversas abordagens para se calcular os coeficientes \(\alpha\) e \(\beta\) da equação da regressão linear, as técnicas baseadas em mínimos quadrados ordinários e gradiente descendente são as mais comuns. A seguir serão apresentados os funcionamentos dessas abordagens.

2.1.1.1 Métodos dos quadrados ordinários

O Método dos quadrados ordinários (MQO) ou método dos mínimos quadrados (MMQ), busca encontrar o melhor valor para os coeficientes citados anteriormente, de tal forma que a diferença absoluta entre o valor real e o predito pela função seja a menor possível entre todos os pontos. A Figura 2.3 mostra um exemplo de regressão linear utilizando o MQO para o conjunto de pontos descritos na tabela a seguir:

Variável independente	Variável dependente
0,44	5,52
1,74	8,89
0,41	4,05
1,84	9,31
0,98	6,57
1,22	8,27
1,53	6,93
1,04	6,41
0,59	6,93
0,38	6,98

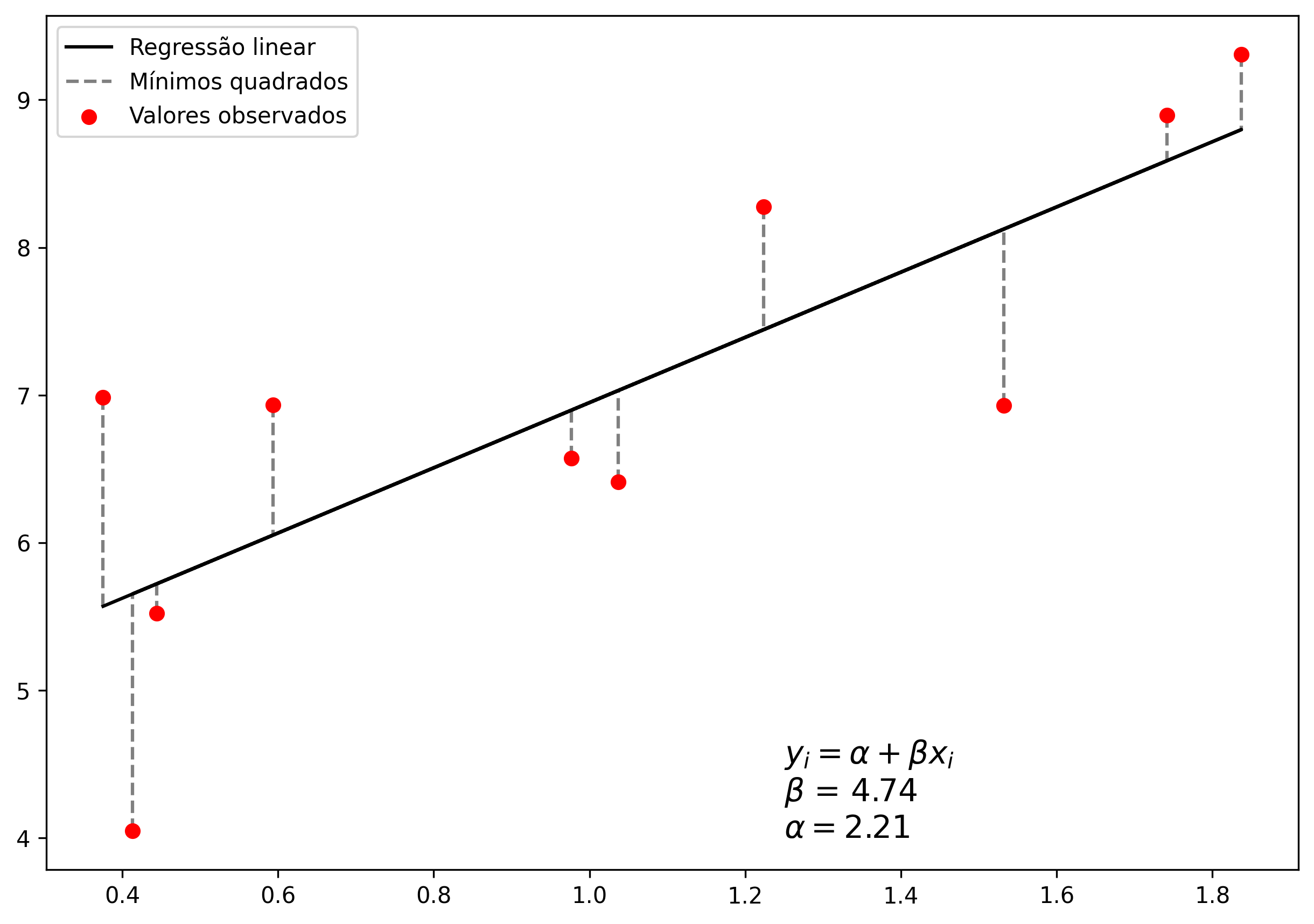
Figure 2.3: Exemplo do método dos quadrados ordinários.

Para se chegar no resultado apresentado na Figura 2.3, os coeficientes da regressão linear foram ajustados utilizando derivadas parciais, de tal tal forma que o erro quadrático médio entre entre a função e cada um dos pontos fossem a menor possível. A Figura 2.4 mostra o ajuste dos coeficientes da equação em relação a cada ponto.

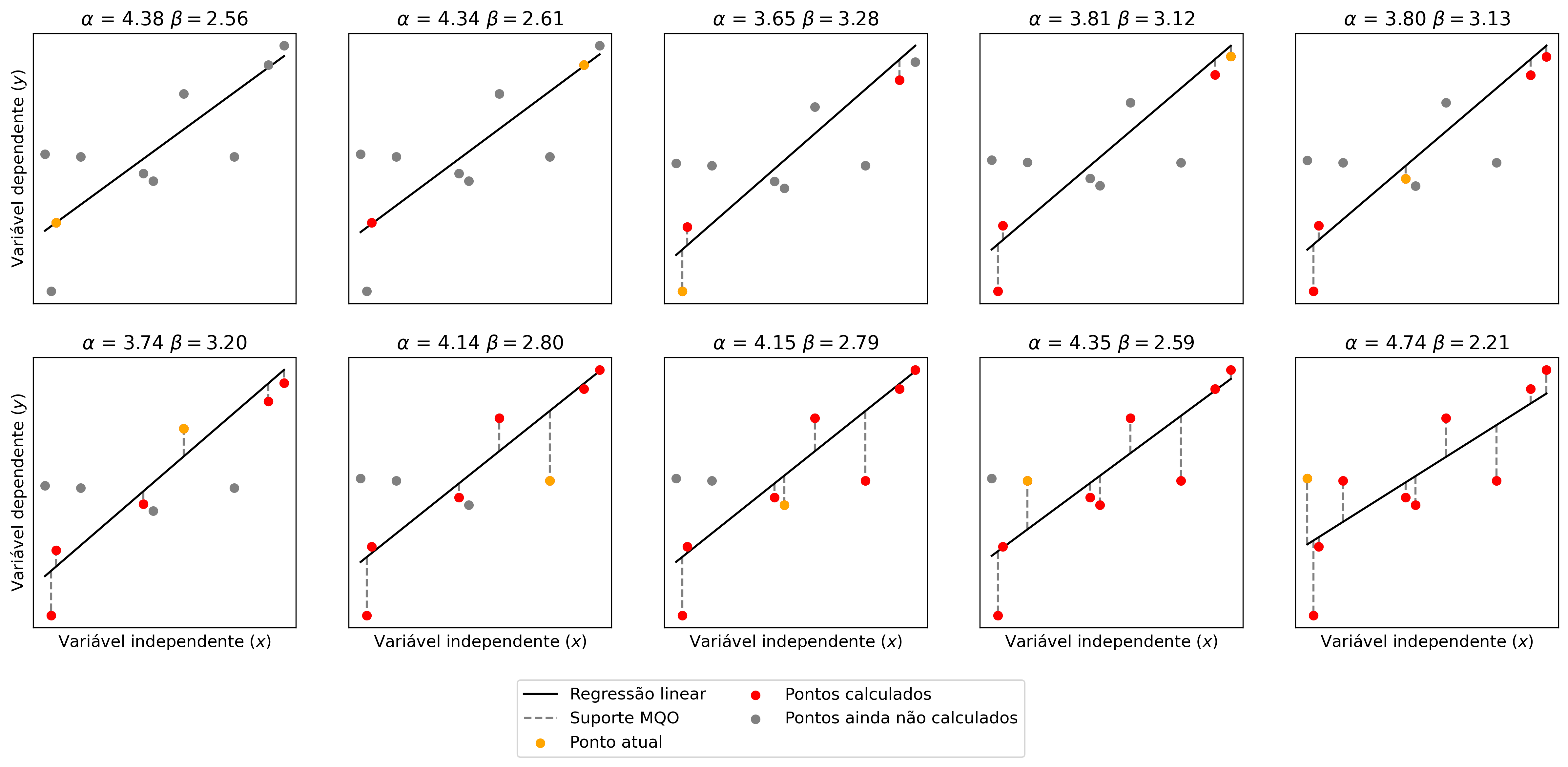
Figure 2.4: Ajuste da regressão linear por método dos quadrados ordinários.

2.1.1.2 Gradiente descendente

O método do gradiente descendente (GD) é uma das técnicas mais utilizadas para otimização de modelos de ML. Este é um método interativo que busca encontrar os coeficiente \(\alpha\) e \(\beta\) através da minimização de uma função de custo, que normalmente é o erro quadrático médio (MSE - sigla do inglês, mean squared error).

O GD funciona de forma iterativa e inicializa os coeficientes com um valor predefinido ou aleatório. Em cada iteração é obtido o somatório do erro entre todos os valores das variáveis dependentes e valores calculados pela função. Com base nesse erro e em uma taxa de aprendizagem do modelo pré definida, os valores dos coeficientes da função são atualizados para a próxima iteração. A taxa de aprendizagem deve ser definida com um valor equilibrado. A definição de um valor muito alto para a taxa de aprendizagem pode levar o modelo a cair em um mínimo local, ou seja, o modelo não consegue chegar em seu melhor ajuste. Já quando a taxa de aprendizagem é definida com um valor muito baixo, o modelo demora mais tempo para chegar no ajuste ideal, necessitando de muito mais tempo e processamento até que haja a convergência. A Figura 2.5 mostra o comportamento do GD com diferentes categorias de valores mencionadas para a taxa de aprendizagem.

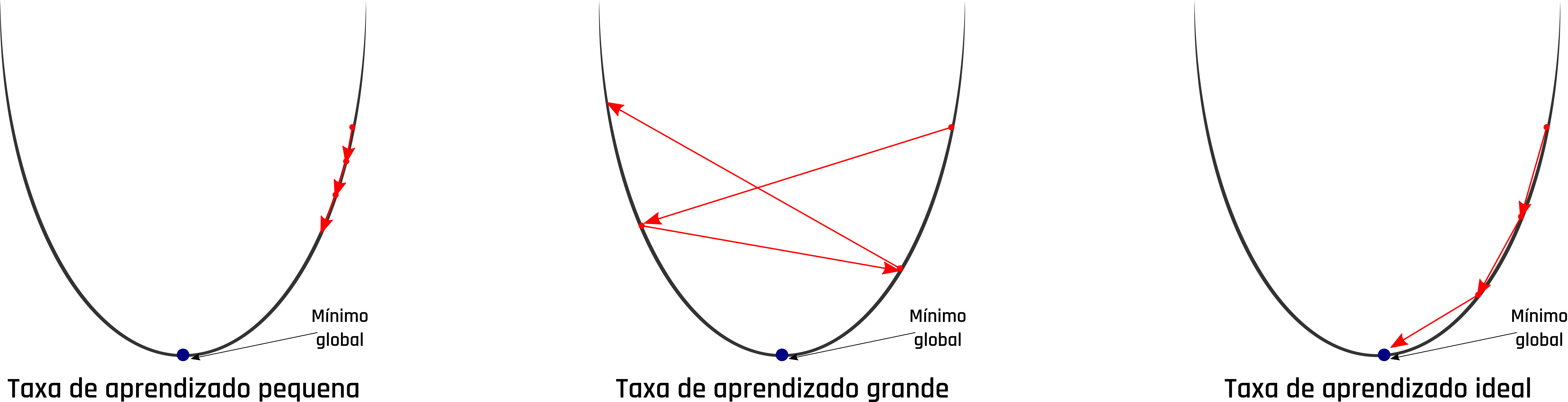
Figure 2.5: Problemas na taxa de aprendizado do gradiente descendente.

Os principais parâmetros a serem definidos nessa abordagem são a taxa de aprendizagem e o número de iterações. Considerando os pontos utilizados no exemplo anterior, foi aplicada a regressão linear utilizando o GD como método de atualização dos coeficientes. A Figura 2.6 mostra o ajuste da função, custo e os coeficientes \(\alpha\) e \(\beta\) ao longo de 50 iterações com taxa de aprendizado muito baixa. Na Figura 2.6 pode ser observado que as iterações finalizam antes da convergência do modelo.

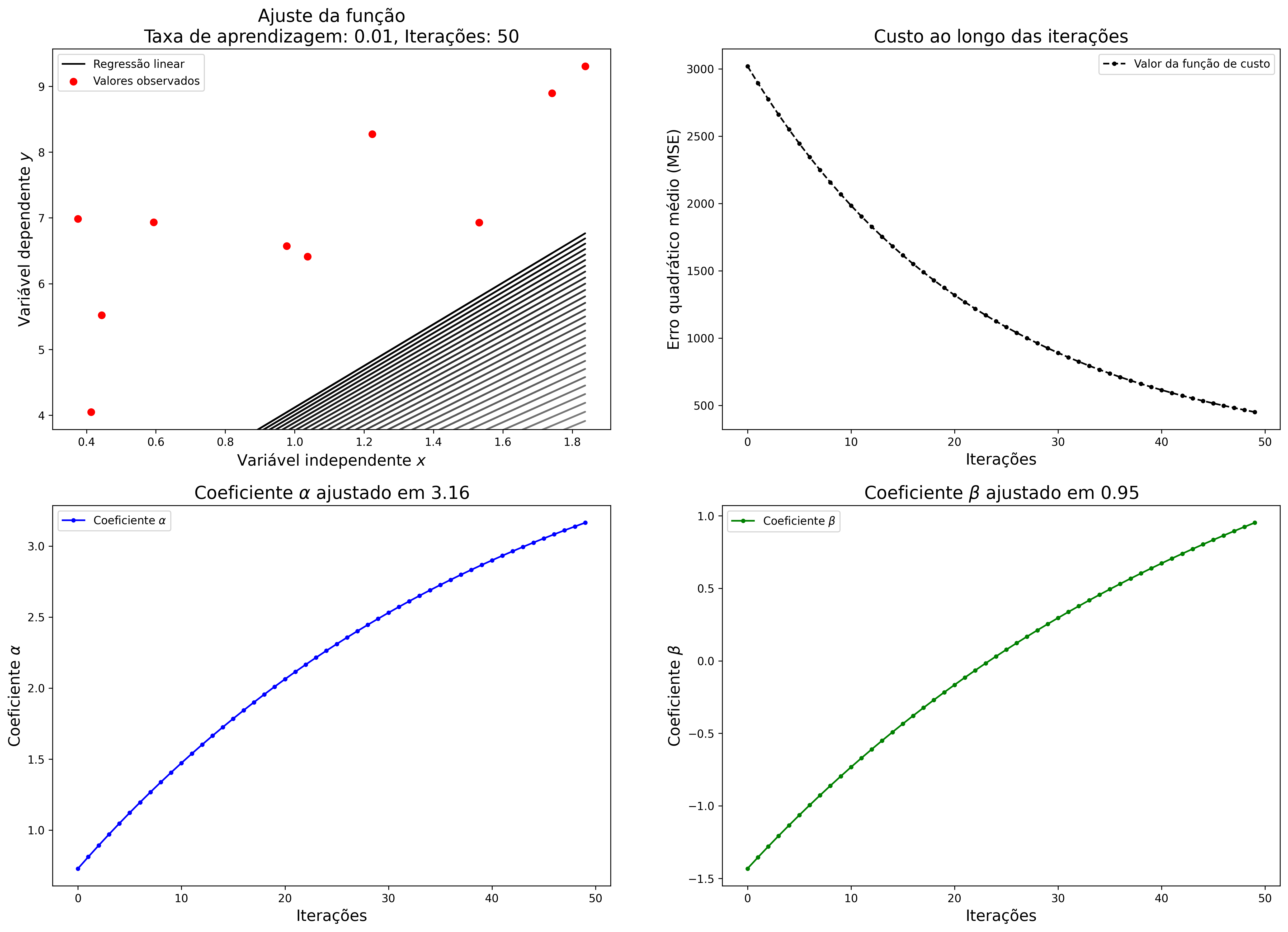
Figure 2.6: Regressão linear com taxa de aprendizagem baixa no gradiente descendente.

Como mencionado anteriormente, uma taxa de aprendizagem muito grande também interfere no ajuste dos coeficientes, uma vez o modelo não consegue atingir o mínimo global. A Figura 2.7 mostra o resultado da execução da regressão linear utilizando uma taxa de aprendizagem muito grande no GD.

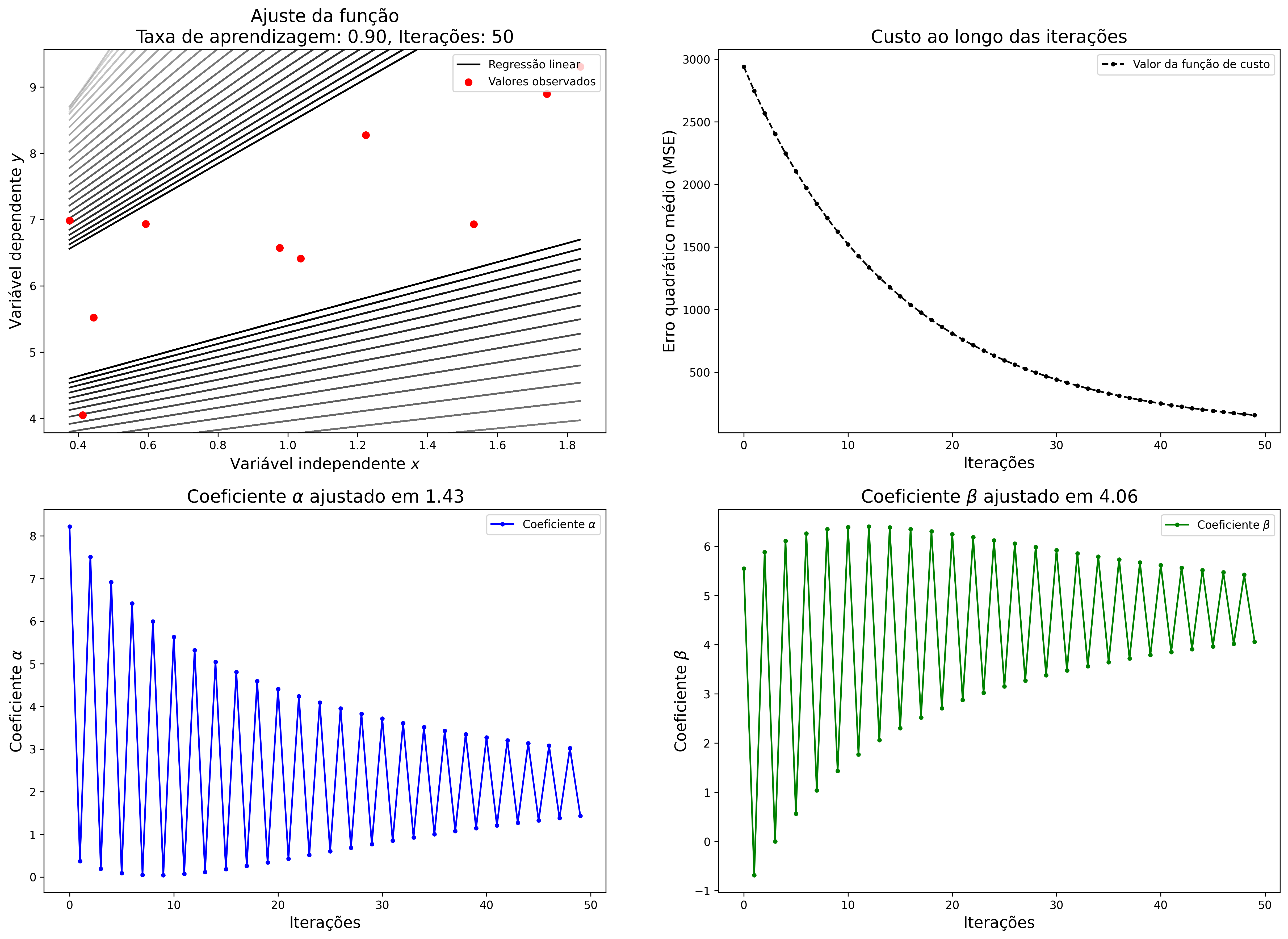
Figure 2.7: Regressão linear com taxa de aprendizagem alta no gradiente descendente.

Já com uma taxa de aprendizagem equilibrada, o GD é capaz de ajustar os coeficientes de forma mais eficiente. A Figura 2.8 mostra o resultado do algoritmo executado com uma taxa de aprendizagem mais equilibrada. Como os valores iniciais dos coeficientes são definidos de forma aleatória, nas primeiras iterações o gradiente apresenta uma alta perturbação, que vai se atenuando ao longo das épocas.

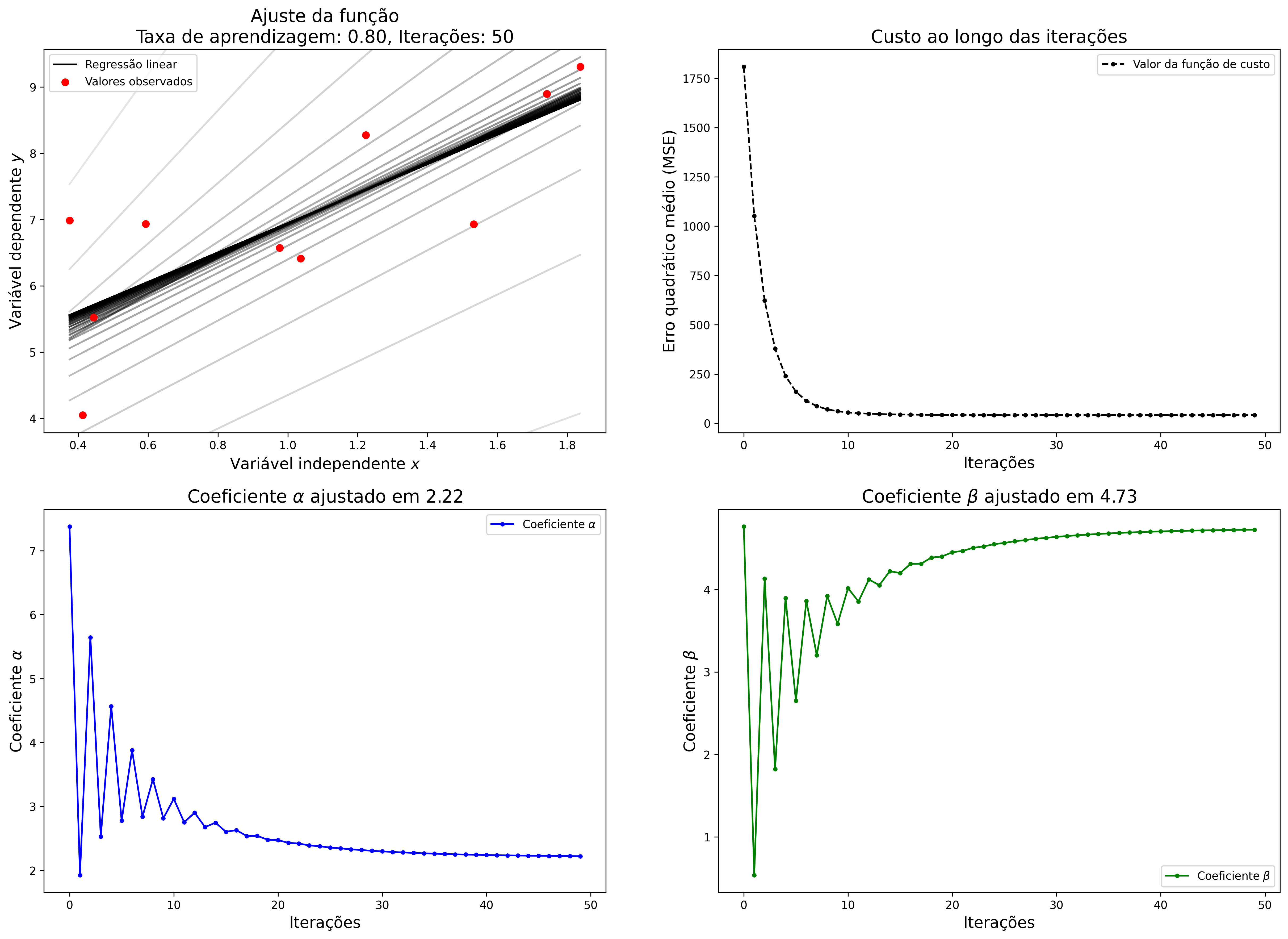
Figure 2.8: Regressão linear com taxa de aprendizagem equilibrada no gradiente descendente.

Para dados com poucas dimensões, ou seja, poucas variáveis preditoras, o MQO é mais recomendado, pois diferente do GD, não é um algoritmo interativo, e sua complexidade está associada diretamente à quantidade de pontos. Já o GD tem melhor performance quando os dados possuem muitas dimensões.

A regressão linear pode ser aplicada em uma vasta variedade de problemas, mas como foi apresentado ao longo desta seção, é necessário que os dados possuam uma alta correlação para ela funcionar perfeitamente bem. Este algoritmo está implementado nas principais principais bibliotecas de ML em diferentes linguagens de programação. Em Python a regressão linear está disponível na biblioteca Scikit-learn.

2.2 Máquina de vetores de suporte

A máquina de vetores de suporte (SVM - sigla do inglês, support vector machine) é um modelo de aprendizado de máquina supervisionado concebido a partir de um conceito inicialmente proposto por Vapnik and Chervonenkis (1963). A SVM podem ser utilizada tanto para tarefas de classificação, quanto para tarefas de regressão, sendo uma ótima alternativa aos modelos de redes neurais artificiais profundas que tem custo computacional muito superior em dados com muitas dimensões. Outra vantagem na utilização dos modelos baseados em SVM é que eles não são sensíveis aos outliers, ou seja, valores extremos não causam ruído no treinamento.

O funcionamento básico das SVM consiste em ajustar a equação de uma reta, denominada hiperplano de tal forma que a distância entre ela e os pontos com características diferentes seja maximizada. Um conjunto de \(n\) pontos é definido como \((\vec{x_{1}}, y_{1}), (\vec{x_{2}}, y_{2}), ..., (\vec{x_{n}}, y_{n})\), onde \(\vec{x_{i}}\) são as variáveis independentes representadas por um vetor de \(d\)-dimensões e \(y_{i}\) são as variáveis dependentes. A distância maximizada entre o hiperplano e as fronteiras são definidas como margens e os pontos que estão no limite dessa margem são os vetores de suporte. Esses componentes podem ser modelados da seguinte forma:

\[\begin{equation} \vec{w}\cdot\vec{x}-b = \begin{cases} & -1, & \text{primeiro vetor de suporte} \\ & 0, & \text{hiperplano} \\ & 1, & \text{segundo vetor de suporte} \end{cases} \tag{2.4} \end{equation}\]

Onde \(\vec{w}\) é um vetor perpendicular aos pontos, \(\vec{x}\) é o vetor do conjunto de pontos é \(b\) é uma constante opcional que pode ser usada como uma bias. Quando o resultado dessa equação é igual a \(1\) ou \(-1\) trata-se de um dos vetores de suporte, já com o resultado maior que \(0\) e menor que \(1\) ou menor que \(0\) e maior que \(-1\) trata-se de um espaço da margem. A Figura 2.9 mostra um exemplo da aplicação do algoritmo SVM em um conjunto de dados linearmente separável. Nessa figura, o hiperplano é caracterizado pela linha contínua, os vetores de suporte são as linhas tracejadas que interceptam os pontos com contorno destacado, e o espaço entre eles são as margens.

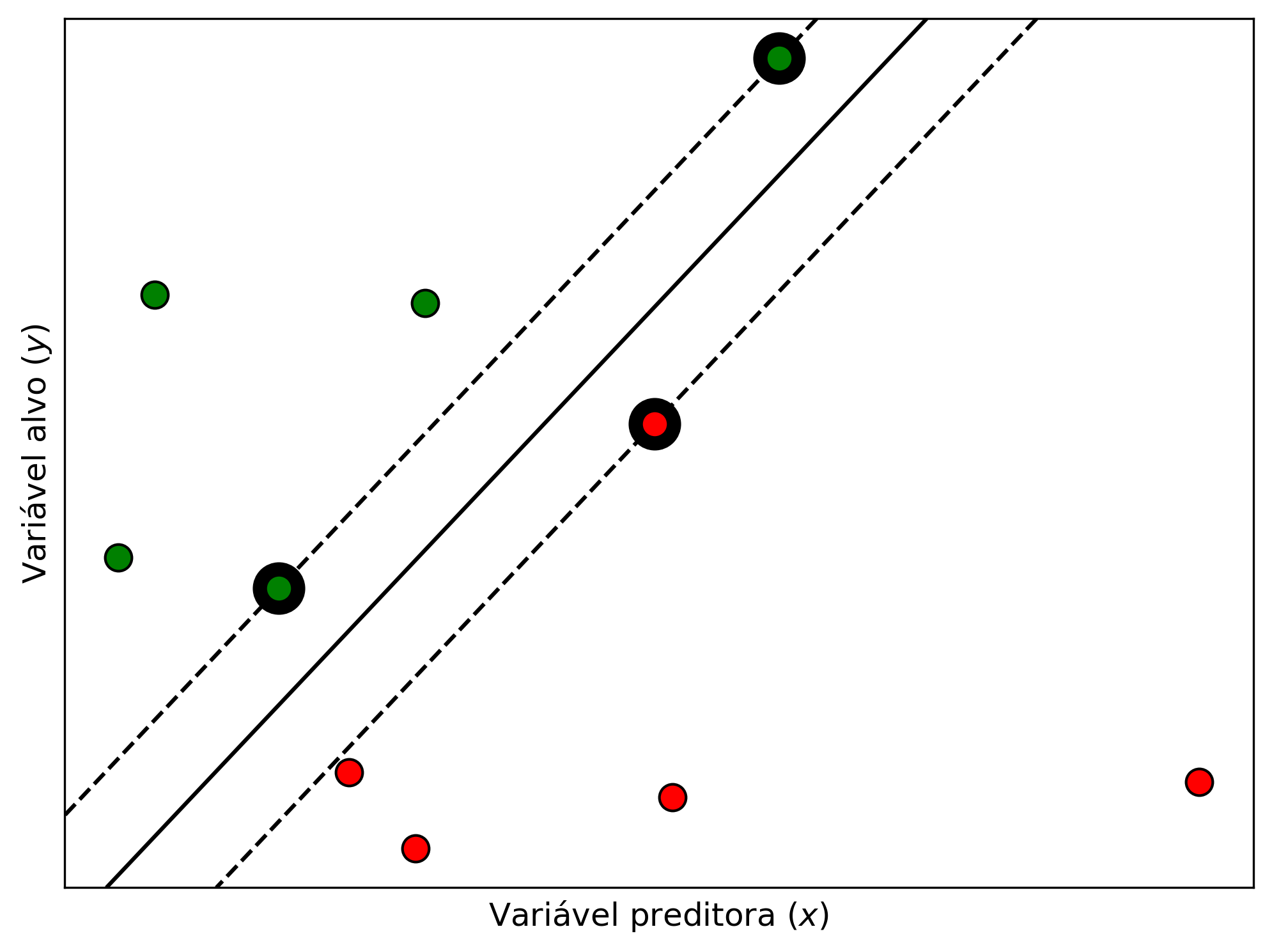
Figure 2.9: SVM para conjunto de dados linearmente separáveis.

As primeiras versões das SVM eram limitadas somente para resolução de problemas linearmente separáveis, como mostrado no exemplo anterior, mas a grande maioria dos problemas não são linearmente separáveis. Considerando a Figura 2.10 é muito difícil traçar um hiperplano que separe bem os pontos de cores diferentes. Uma alternativa para esse problema é aumentar as dimensões para a representação do hiperplano. Essa tarefa é feita com a introdução de um conceito definido kernel.

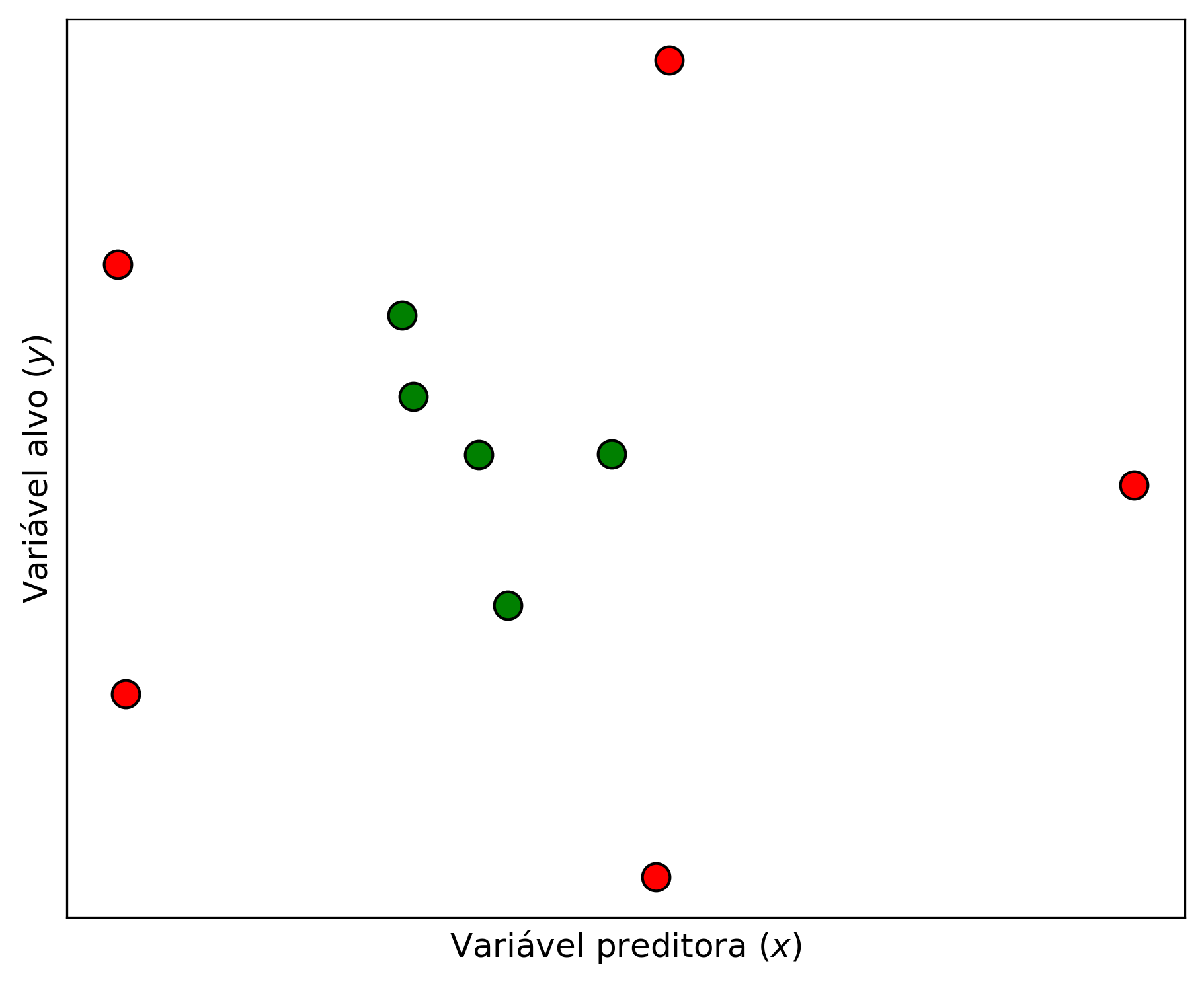
Figure 2.10: Conjunto de dados não linearmente separáveis.

Ao traçar um hiperplano não linear com a utilização de kernels é possível ajustar melhor os vetores de suporte aos dados. A Figura 2.2.1 mostra o conjunto de dados ajustado com hiperplanos lineares e não lineares.

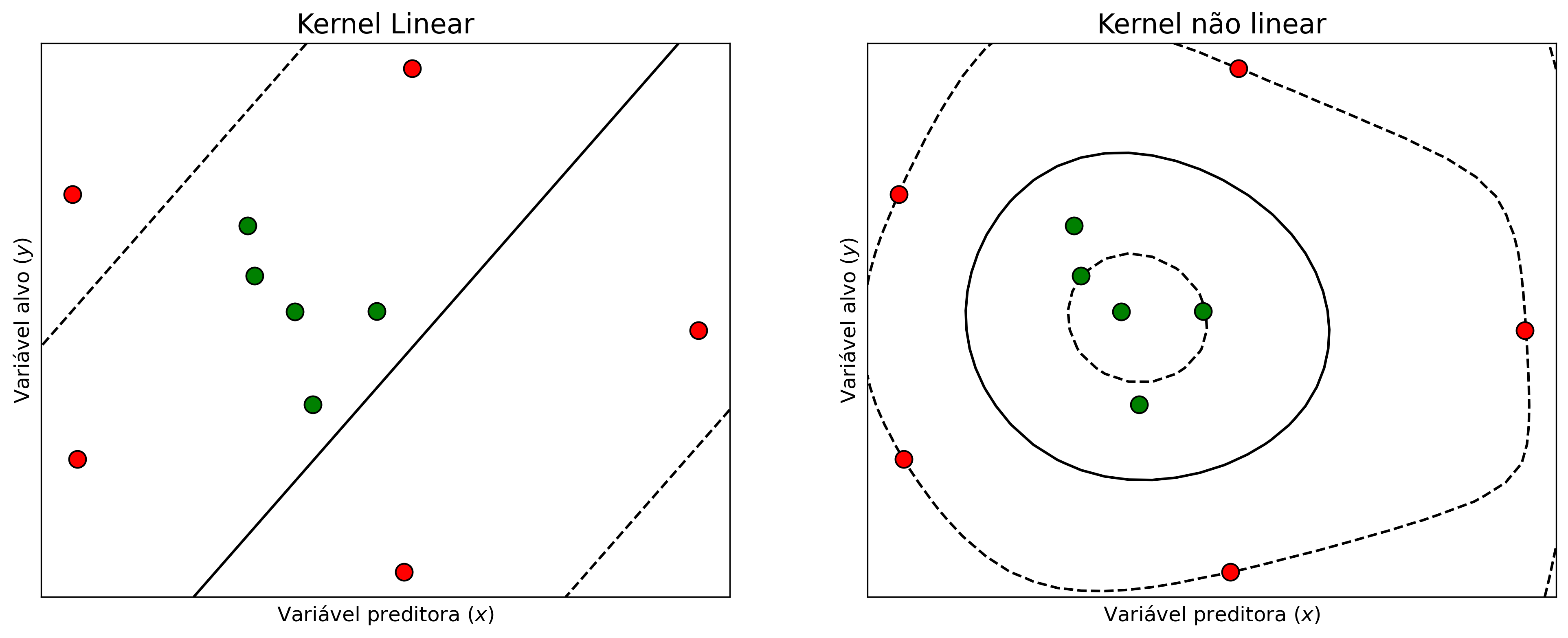
Figure 2.11: Hiperplanos utilizando kernels com funções lineares e não lineares.

A abordagem utilizando os kernels é uma das principais características desse modelo de ML, pois faz com que o hiperplano seja ajustado em uma dimensão superior, utilizando equações de polinômios de grau maior. A Figura 2.12 mostra graficamente como é realizada essa manipulação.

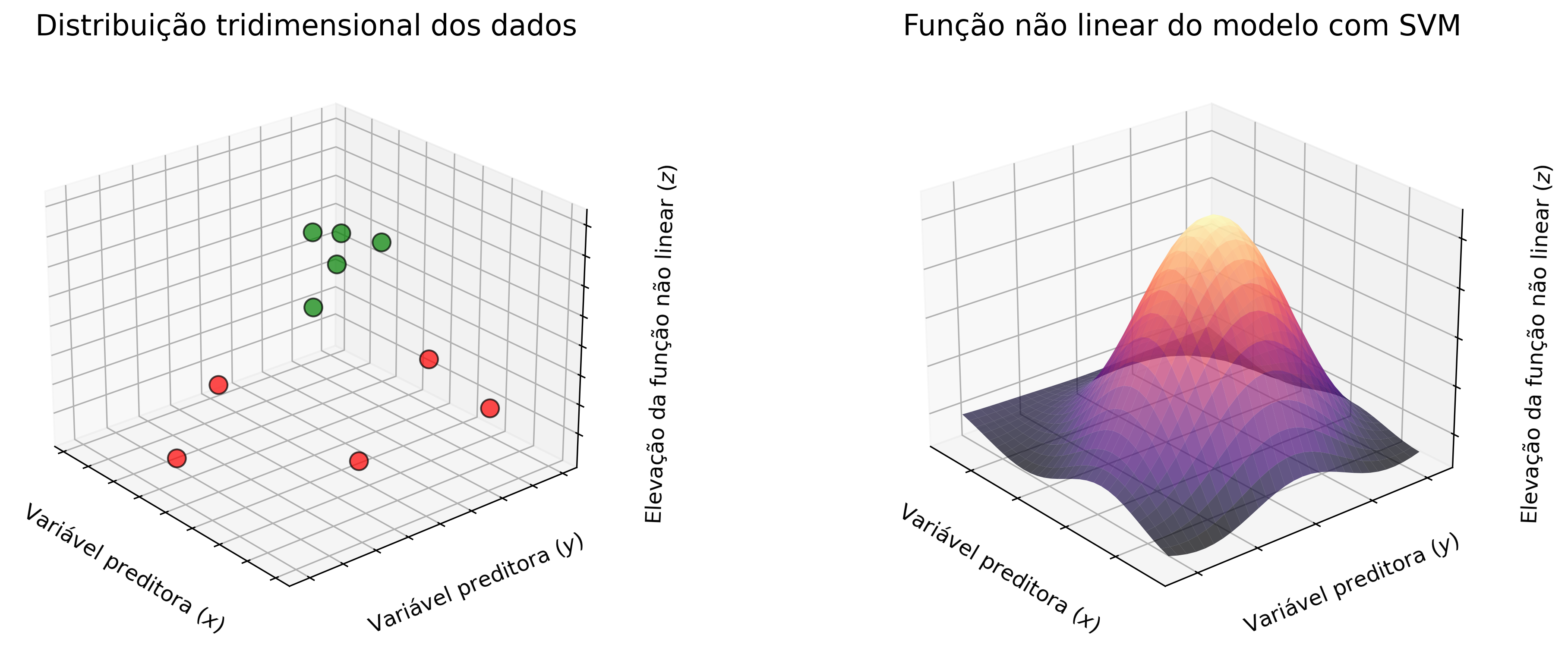
Figure 2.12: Representação gráfica dos dados e da função não linear.

A utilização de kernels é uma das principais características do SVM e faz com que os modelos baseados nessa abordagem, sejam tão robustos quanto outras técnicas mais complexas.

2.2.1 Kernels

A utilização dos kernels em SVM foram introduzidos por Boser, Guyon, and Vapnik (1992). Kernels são responsáveis por criar uma transformação dos dados a partir de uma função, que são responsáveis por maximizar as margens dos vetores de suporte. A maioria das bibliotecas de ML, já possuem kernels implementados e também permitem a integração de outras funções customizadas. A lista a seguir apresenta brevemente alguns dos principais kernels utilizados.

• Linear: Como mencionado anteriormente, é eficiente somente para problemas linearmente separáveis, uma vez que seu ajuste se da através da equação de uma reta. O kernel linear é definido apenas pelo produto entre duas amostras \(\vec{x_{i}}\) e \(\vec{x_{j}}\):

\[\begin{equation} k(\vec{x_{i}}, \vec{x_{j}}) = \vec{x_{i}} \cdot \vec{x_{j}} \tag{2.5} \end{equation}\]

• Polinomial: Os kernels polinomiais popularmente utilizados em tarefas de processamento de imagens, permitem adicionar curvas aos hiperplanos. Além das amostras \(\vec{x_{i}}\) e \(\vec{x_{j}}\), o kernel polinomial também recebe o a variável \(d\) que indica o seu grau, como definido pela equação:

\[\begin{equation} k(\vec{x_{i}}, \vec{x_{j}}) = (\vec{x_{i}} \cdot \vec{x_{j}} + 1)^{d} \tag{2.6} \end{equation}\]

• Função gaussiana de base radial: Os kernels RBF (radial basis function), como também são chamados, são recomendados quando não se tem um conhecimento prévio acerca dos dados. Esse kernel realiza uma transformação dos pontos utilizando uma função gaussiana, definida por:

\[\begin{equation} k(\vec{x_{i}}, \vec{x_{j}}) = exp \left(-\frac{\lVert\vec{x_{i}} - \vec{x_{j}}\rVert^2}{2\sigma^2} \right) \tag{2.7} \end{equation}\]

2.2.2 Regressão com máquinas de vetores de suporte

Embora a SVM seja aplicada principalmente para tarefas de classificação, ou seja, geração de variáveis categóricas, ela também pode ser utilizada para tarefas de regressão, calculando valores reais a partir de uma mudança na sua função objetivo (Drucker et al. 1997). Essas abordagens são chamadas de regressão por vetores de suporte (SVR - sigla do inglês, support vector regression) e foram propostas por Drucker et al. (1997). Diferente de modelos tradicionais como as técnicas de regressão apresentadas na seção anterior, que utilizam derivadas parciais para os cálculos dos intervalos de confiança, no SVR os valores são previstos através dos hiperplanos.

Este método utiliza para a regressão a abordagem de classificação apresentada anteriormente, porém com uma pequena variação na função objetivo, que agora busca comportar dentro das margens comportar a maior quantidade de pontos. As margens (\(\epsilon\)) representam os intervalos de confiança e os vetores de suporte que as delimitam, representam os limites para os erros positivos (\(\xi\)) e negativos (\(\xi^{\ast}\)). A Figura 2.13 mostra uma representação de um hiperplano não linear traçado para a regressão de dados.

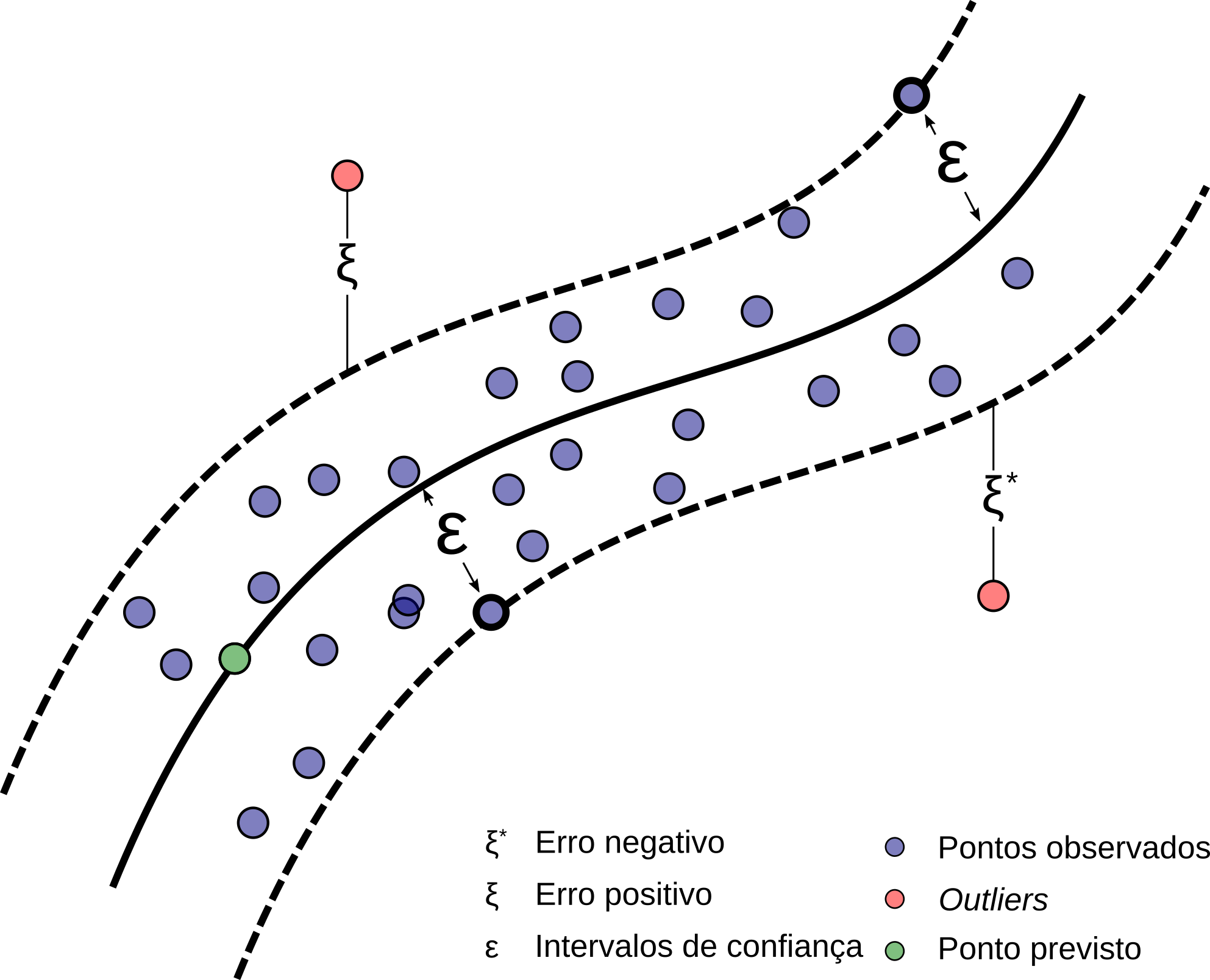
Figure 2.13: Representação de hiperplano não linear para regressão. Adaptado de Drucker et al. (1997).

Referências Bibliográficas

Boser, Bernhard E, Isabelle M Guyon, and Vladimir N Vapnik. 1992. “A Training Algorithm for Optimal Margin Classifiers.” In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, 144–52.

Drucker, Harris, Christopher JC Burges, Linda Kaufman, Alex J Smola, and Vladimir Vapnik. 1997. “Support Vector Regression Machines.” In Advances in Neural Information Processing Systems, 155–61.

Helliwell, John F, Haifang Huang, Shun Wang, and Max Norton. 2020. “Social Environments for World Happiness.” World Happiness Report 2020.

Kirch, Wilhelm, ed. 2008. “Pearson’s Correlation Coefficient.” In Encyclopedia of Public Health, 1090–1. Dordrecht: Springer Netherlands. https://doi.org/10.1007/978-1-4020-5614-7_2569.

Soto, Timothy. 2013. “Regression Analysis.” In Encyclopedia of Autism Spectrum Disorders, edited by Fred R. Volkmar, 2538–8. New York, NY: Springer New York.

Vapnik, Vladimir N, and Alexey Y Chervonenkis. 1963. “On a Class of Pattern-Recognition Learning Algorithms.” Automation and Remote Control 25 (6). PLENUM PUBL CORP CONSULTANTS BUREAU, 233 SPRING ST, NEW YORK, NY 10013: 838.