4 Agrupamento

Afinal, todos nós nos enquadramos em um grupo. - (autor desconhecido)

Vimos até agora que os métodos de classificação e regressão usam conjuntos de dados rotulados e usamos tais métodos para encontrarmos modelos que descrevem nossos dados. Em resumo, os métodos de classificação realizam a predição de dados categóricos, de modo oposto, os métodos de regressão fazem a predição de dados contínuos, sendo que ambos precisam à priori dos rótulos para criarem seus modelos.

As técnicas de agrupamento operam de modo diferente do que foi visto até então, pois usam conjunto de dados não rotulados, o que modifica a forma com que os métodos aprendem. É isso que vamos ver neste capítulo!

Neste capítulo, vamos aprender o que é um agrupamento e suas técnicas, com exemplos práticos usando as linguagens de programação R e Python na plataforma Kaggle. Vamos começar respondendo à pergunta:

“O que é um agrupamento?”

4.1 O que é um agrupamento?

Para entendermos o conceito de agrupamento, vamos começar com um exemplo prático. Digamos que você tenha um amigo que adora livros, e ele tem muitos deles, mas tem muitas dificuldades em organizá-los. Então, você, uma pessoa muito disposta, sugere ao seu amigo algumas formas de como organizar esses livros, por exemplo: separá-los por gênero, cores ou ordem alfabética. Aderindo às suas dicas, seu amigo decidiu agrupá-los por gênero. Assim, com essa nova organização foi possível encontrar diversos grupos de livros separados por gênero, como apresentado na Figura 4.1.

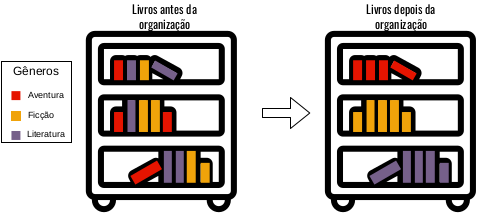
Figure 4.1: Antes e depois da organização da prateleira de livros em grupos baseados em gênero.

Utilizamos cores para dividir os gêneros na Figura 4.1 apenas para facilitar a vida do design.

A partir do exemplo acima, vimos que os grupos foram criados de acordo com uma característica, neste caso, gênero, mas poderíamos ter grupos de livros organizados com mais de uma característica. Por exemplo, grupos com livros do mesmo gênero e o mesmo ano de lançamento, ou do mesmo gênero e com a mesma cor, e assim por diante. Assim, podemos concluir que livros pertencentes ao mesmo grupo são semelhantes entre si, ou seja, possuem características iguais ou parecidas, mas são diferentes se comparados com livros de outros grupos. Com isso, aprendemos um conceito fundamental em Agrupamento, que é a definição de um grupo.

Em aprendizado de máquina, o ato de separar objetos em grupos (em inglês, clusters) por meio de determinadas características de um conjunto de dados é conhecido como agrupamento (em inglês, clustering), e a maneira com que esses grupos são separados é chamado de técnicas ou métodos de agrupamento. De modo oposto do que vimos nos capítulos anteriores, as técnicas de agrupamento possuem o aprendizado não supervisionado, ou seja, usam conjuntos de dados não rotulados para criarem seus modelos.

Diante da vasta quantidade de dados gerados diariamente, provindos de diferentes fontes, como radares, redes sociais e smartphones, torna-se cada vez mais difícil obter conjuntos de dados rotulados, pois, por vezes, é necessária a presença de um especialista para criar ou gerenciar esses rótulos. Desta forma, o uso de técnicas de agrupamento pode auxiliar no processo de descoberta de padrões e na criação de novos rótulos a partir de grupos gerados em um agrupamento.

Técnicas de agrupamento caem como luva na mão de cientistas e analista de dados, uma vez que identificam padrões em conjuntos de dados através da organização dos dados em grupos. Em detalhes, os grupos são formados por objetos que possuem a máxima semelhança entre si, e a mínima semelhança com elementos de outros grupos (Aghabozorgi, Shirkhorshidi, and Wah 2015) - como vimos no exemplo dos livros. Para identificar esse grau de semelhança entre os objetos precisamos de uma medida de similaridade, pois é ela que vai nos dizer o quão parecidos ou não são os objetos que desejamos agrupar. Para isto, medidas de distância são usadas para determinar tal similaridade, por exemplo, a distância euclidiana entre os pontos de dois objetos.

Explicamos a diferença entre cientista e analista de dados no nosso minicurso de Introdução à análise de dados.

Na Figura 4.2 vemos dois exemplos de agrupamentos em um espaço com duas dimensões (\(X\) e \(Y\)). O primeiro agrupamento 4.2(a) possui 3 grupos e o segundo 8 4.2(b). Note que o termo objeto refere-se a uma linha do conjunto de dados, conforme ilustrado, em que um objeto no Grupo 8 possui os valores de \(X = 8\) e \(Y = 8\).

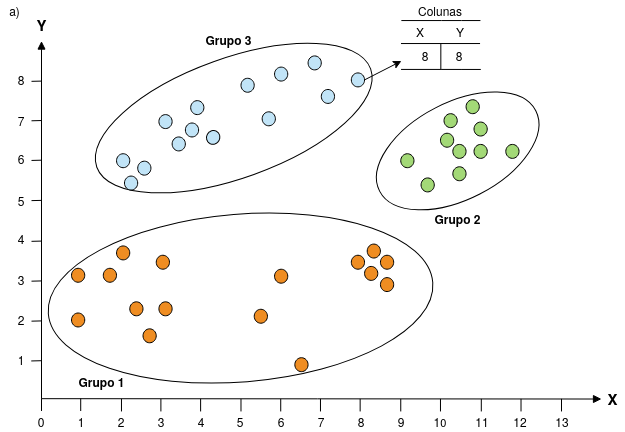
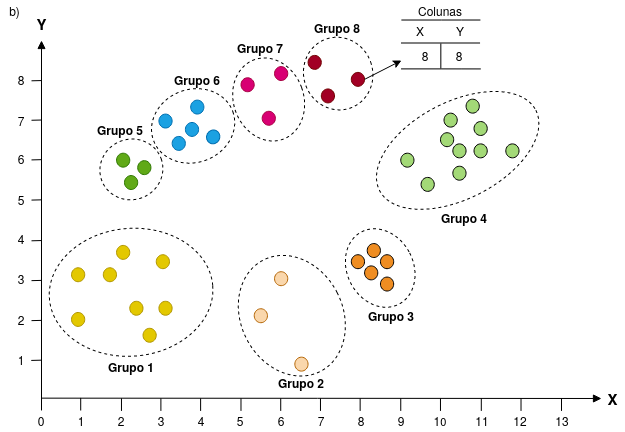
Figure 4.2: Exemplo de dois agrupamentos em um plano com duas dimensões (X,Y). Observam-se 3 grupos em a) e 8 grupos em b). Adaptado de Esling and Agon (2012)

De acordo com Jain (2010), um dos grandes estudiosos da área de aprendizado de máquina, o uso de técnicas agrupamento podem ser divididos em três principais aplicações:

• Descoberta de conhecimento em estruturas intrínsecas: para obter informações sobre dados, gerar hipóteses, detectar anomalias e identificar características salientes.
• Classificação natural: por exemplo, na Biologia, para identificar o grau de semelhança entre formas ou organismos (relação filogenética).
• Compressão: como um método para organizar os dados e resumi-los através de protótipos de agregados.

Além das aplicações mencionadas por Jain (2010), como descoberta de padrões, detecção de outliers e análise de distribuições intrínsecas nos dados; segundo Han, Pei, and Kamber (2011), às técnicas de agrupamento podem ser usadas em etapas de pré-processamento para outros algoritmos, por exemplo, na caracterização, seleção de subconjuntos de atributos e classificação. Desta forma, diante dessas aplicações, o uso de técnicas de agrupamento encontra-se em diversas áreas do conhecimento, entre elas: Biologia: (Gasch and Eisen 2002), Sensoriamento Remoto: (He et al. 2014) e business intelligence: (Wang, Wu, and Zhang 2005).

Agora que entendemos o que é um agrupamento e suas aplicações, na próxima subseção vamos mostrar algumas técnicas de agrupamento e quais as principais diferenças entre elas.

4.2 Técnicas de agrupamento

Como vimos anteriormente, cada técnica de agrupamento possui uma abordagem para criar grupos em um conjunto de dados, por exemplo, algumas técnicas são baseadas em pontos centrais de cada grupo (centróide); em outras os grupos são criados seguindo uma hierarquia presente nos dados. Neste minicurso, vamos mostrar duas abordagens de técnicas de agrupamento: baseadas em partição e hierarquia. A seguir vamos comentar de maneira geral cada uma.

4.2.1 Técnicas baseadas em Partição

Nas técnicas baseadas em partição cada grupo representa uma partição, sendo que o número de grupos é definido pelo usuário. Desta forma, cada partição deve conter pelo menos um objeto, e cada objeto deve pertencer somente a um grupo, o que é conhecido como separação exclusiva de grupos (em inglês, exclusive cluster separation ou hard cluster). Existem métodos que flexibilizam o critério de separação exclusiva, sendo assim, o objeto possui porcentagens de pertencimento a cada grupo, o que é conhecimento como técnicas de agrupamento nebulosas (em inglês, fuzzy clustering). A Figura 4.3 mostra um exemplo de agrupamento baseado em partição, as linhas pretas demarcam cada partição.

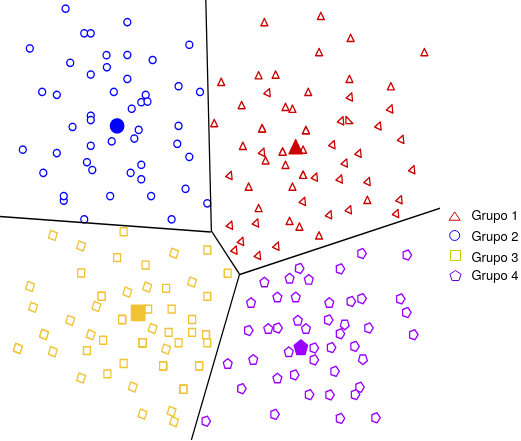
Figure 4.3: Exemplo de um agrupamento baseado em partição. As linhas pretas demarcam as partições e as formas geométricas preenchidas os centróides. Adaptado de Developers (2020)

Além das características mencionadas acima, grande parte das técnicas baseadas em partição usam medidas de distâncias para determinar o grau de similaridade de cada grupo. Outra característica importante de mencionar é a representação de cada grupo, o centróide (Figura 4.3), que pode ser definido pela média ou qualquer outra medida estatística. Um dos algoritmos mais utilizados baseados em partição é o Kmeans - vamos explicá-lo nas próximas páginas.

4.2.2 Técnicas baseadas em Hierarquia

Nas técnicas baseadas em hierarquia, diferente do que vimos nas técnicas de partição, não é requerido que o especialista especifique o número de grupos, pois seu algoritmo busca por correlações entre os objetos do conjunto de dados para criar os grupos. Baseado no modo em que sua decomposição hierárquica é formada, os métodos hierárquicos podem ser divididos em aglomerativos ou divisivos. No método aglomerativo, também conhecido como AGNES (do inglês, Agglomerative Nesting), considera-se, inicialmente, que cada objeto seja seu próprio grupo, e a cada iteração, os dois grupos mais parecidos são unidos, assim, formando um novo um grupo. Esse processo é repetido até que todos os objetos estejam em um único grupo. De modo oposto, o método divisivo, também conhecido como DIANA (do inglês, Divise Analysis), considera-se que todos objetos pertencem a um único grupo, e posteriormente, o único grupo é dividido até obter-se um grupo para cada objeto ou até que um critério de párada seja atendido (Han, Pei, and Kamber 2011).

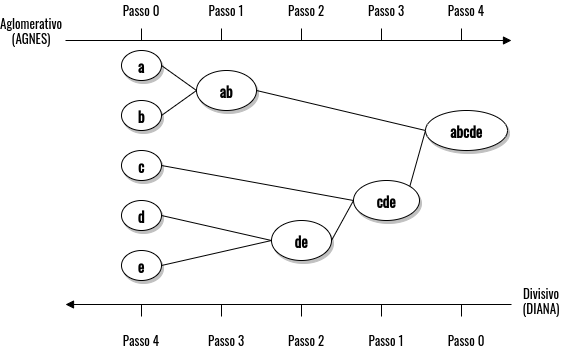
Figure 4.4: Exemplo do processo de criação de grupos baseado nas técnicas de agrupamento hierarquicas. - Fonte: Han, Pei, and Kamber (2011)

Na Figura 4.4 é possível observar o processo de criação de grupos dos dois métodos mencionados, AGNES e DIANA, com base em um conjunto de dados com cinco objetos \(a, b, c, d, e\). Por exemplo, no método aglomerativo, o objeto \(a\) junta-se com o objeto \(b\) no mesmo grupo, pois possuem maior semelhança se comparados com outros objetos, o mesmo processo acontece com os objetos \(d\) e \(e\). Por outro lado, o método divisivo inicia-se com todos os objetos pertencendo a um grupo, e a cada passo vai se dividindo com base na semelhança dos objetos dentro do grupo.

Uma técnica que auxilia na interpretação dos agrupamentos hierárquicos é o dendrograma, apresentado na Figura 4.5, que faz representação em forma de árvore, nele é possível obter informações sobre a estrutura do agrupamento realizado. No nível 0 é possível observar os objetos em seus próprios grupos, e, conforme o nível da árvore aumenta em relação a sua raiz, menor são as similaridades entre os objetos do mesmo grupo (Han, Pei, and Kamber 2011).

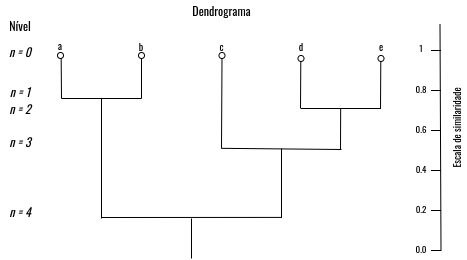
Figure 4.5: Exemplo de representação do agrupamento hierárquico. - Fonte: Han, Pei, and Kamber (2011)

Neste minicurso, vamos abordar o método aglomerativo, no entanto, os mesmos conceitos podem ser aplicados no método divisivo.

4.3 Kmeans

Kmeans ou K-médias é uma técnica de agrupamento que usa o método de partição para dividir o conjunto de dados em \(k\) grupos, em que o valor de \(k\) é definido pelo usuário. De forma geral, o algoritmo do Kmeans visa diminuir a variação intra-grupos, ou seja, criar grupos em que os objetos sejam semelhantes entre si. Então, para que esse objetivo seja atendido, em cada iteração os centróide de cada grupo são atualizados para refinar a qualidade dos grupos.

Posteriormente vamos apresentar algumas heurísticas que auxiliam na determinação do número de grupos

Para exemplificar o funcionamento do Kmeans, vamos usar o conjunto de dados apresentado na Figura 4.6, no qual é possível observar 13 objetos em um plano cartesiano (X,Y).

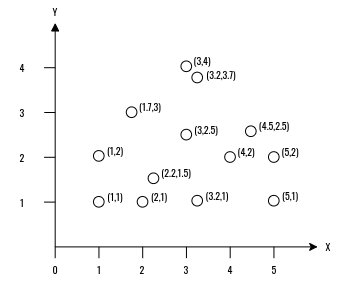
Figure 4.6: Conjunto de dados utilizado como exemplo.

Para separar as observações de forma a obter grupos mais homogêneos, a técnica em questão usa o conceito de centróide, em que é definido um ponto central para cada grupo com base em medidas estatísticas, como a média, e a cada iteração o ponto central é atualizado até que o critério de párada seja alcançado. Então, o primeiro passo do algoritmo é a escolha da quantidade de grupos, neste exemplo, escolhemos três grupos. Com isso, a próxima etapa consiste em sortear, de forma aleatória, o centróides de cada grupo, como apresentado na Figura 4.7. Após o sorteio, os objetos são atribuidos aos seus respectivos grupos, como também apresentado na Figura 4.7. A atribuição é feita com base em uma medida de distância, geralmente, euclidiana; cada objeto é comparado com cada centróide, assim, o objeto é atribuído ao grupo em que possui a menor distância com seu centróide.

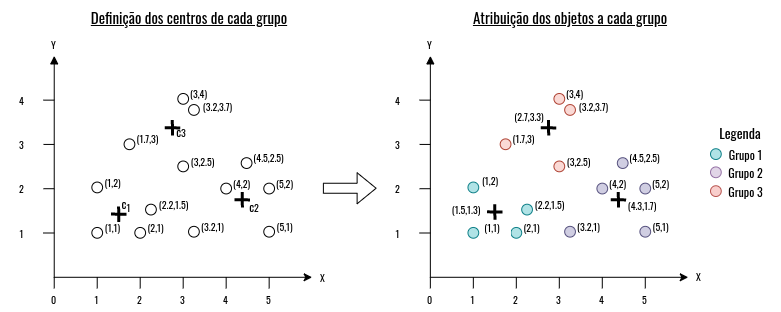
Figure 4.7: Exemplo de funcionamento do algoritmo Kmeans.

Na Figura 4.7 observamos três centróides \(c_1\), \(c_2\) e \(c_3\), nas posições: \((1.5,1.3)\), \((4.3,1.7)\) e \((2.7,3.3)\), respectivamente. Para sabermos em qual grupo o objeto será atribuído basta usar uma medida de distância e verificar qual centróide está mais próximo deste objeto. Por exemplo, seja o objeto que está na posição \((3.2,1)\), temos:

\[ x_{obj} = 3.2\\ y_{obj} = 1.0\\ \\ x_{c1} = 1.5\\ y_{c1} = 1.3\\ \\ x_{c2} = 4.3\\ y_{c2} = 1.7\\ \\ x_{c3} = 2.7\\ y_{c3} = 3.3\\ \\ dist_{c1} = \sqrt{(x_{obj} - x_{c1})^2 + (y_{obj} - y_{c1})^2} \approx 1.73 \\ dist_{c2} = \sqrt{(x_{obj} - x_{c2})^2 + (y_{obj} - y_{c2})^2} \approx 1.30 \\ dist_{c3} = \sqrt{(x_{obj} - x_{c3})^2 + (y_{obj} - y_{c3})^2} \approx 2.35\\ \]

Desta forma, a menor distância (\(dist\)) é dada pelo centróide \(c_2\), então o objeto é atribuído ao grupo deste centróide. Após a atribuição, o centróide é recalculado com base nos objetos do grupo (Figura 4.8). Como foi dito anteriormente, podemos usar medidas estatísticas, como a média para achar a nova posição do centróide. Caso, não haja alterações nos valores dos centróides, o algoritmo pára. Caso não, o processo se repete: os centróides são atualizados e os objetos são atribuídos a cada grupo.

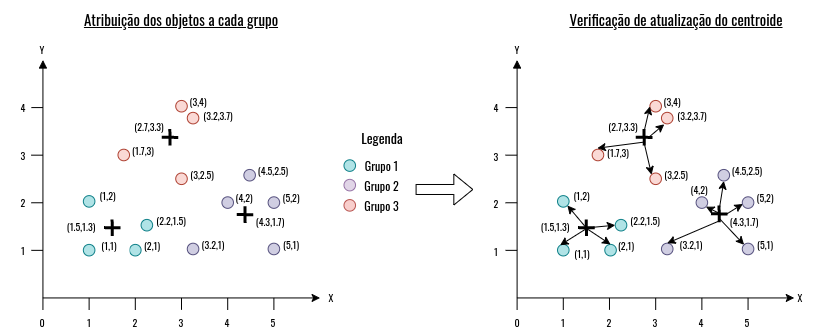
Figure 4.8: Exemplo de funcionamento do algoritmo Kmeans.

Resumidamente, podemos descrever o algoritmo do Kmeans conforme as etapas abaixo:

• (1º Passo) Definição da quantidade de grupos;
• (2º Passo) Sorteio de centróides para cada grupo;
• (3º Passo) Atribuição dos objetos a cada grupo;
• (4º Passo) Atualização dos centróides de cada grupo;
• (5º Passo) Caso os centróides sejam atualizados, volte ao passo (3), caso não, o algoritmo pára.

Lembrando que, outro critério de párada é o número de iterações, pois nem sempre é possível obter grupos homogêneos com poucas iterações. Ainda mais se considerarmos conjuntos de dados de aplicações do mundo real. Outro fato a mencionar, é o sorteio de centróides, pois existem diversas métricas que podem ser utilizadas em relação a inicialização dos centróides, por exemplo, k-means++.

Agora que entendemos mais de perto como o Kmeans funciona. Talvez, você esteja se perguntando: “mas, como verificamos a eficiência do nosso agrupamento?” Isso é o que vamos responder na próxima subseção. Também vamos comentar como podemos estimar o número de grupos em um conjunto de dados.

4.3.1 Como avaliar o Kmeans?

Como mencionado anteriormente, o objetivo do kmeans é minimizar a variação intra-grupos, vimos que isso é feito com base na atualização dos centróides em cada iteração do algoritmo, até que não haja mudança na atualização dos centróides. Então, para verificarmos o erro de cada grupo, podemos usar a soma das diferenças quadráticas (do ingles, sum of squared error) entre cada objeto e o centróide do seu grupo. Por exemplo, na Figura 4.8, para calcularmos o erro quadrático do Grupo 1, temos a seguinte equação:

\[ SSE(grupo_{1}) = \sum_{x_i \in grupo_{1}} dist(x_i - c_1)^2 \]

Em que \(x_i\) representa cada objeto do Grupo 1, \(c_1\) representa o centróide deste mesmo grupo e \(dist\) a medida de distância utilizada. Logo, o \(SSE(grupo_1) \approx 1.9\), em outras palavras, o erro quadrático do Grupo 1 é a soma da distância de todos os objetos em relação seu centróide. Então, para calcularmos o erro total dos grupos, basta fazermos um somatório de cada SSE:

\[ SSE_{total} = SSE(grupo_1) + SSE(grupo_2) + SSE(grupo_3) \]

Desta forma, para este agrupamento apresentado no exemplo acima, temos o \(SSE_{total} \approx x\), em outras palavras, o erro total do nosso agrupamento, é representado pela soma dos erros quadráticos de cada grupo.

Agora que vimos como calcular o erro do nosso agrupamento, só nos resta uma forma de “descobrir” qual a quantidade ideal de grupos para cada agrupamento e é que vamos ver na próxima subseção.

4.3.2 Como definir a quantidade de grupos?

Nesta subseção vamos mostrar dois métodos para definir a quantidade de grupos, sendo eles: Método do Cotovelo e Método da Silhueta.

É recomendado perguntar ao especialista sobre a quantidade de grupos, no caso da ausência de um, podemos optar pelo uso de heurísticas. Duas delas são apresentadas abaixo.

4.3.2.1 Método do cotovelo

O método do cotovelo (do inglês, elbow) usa o somatório do erro total dos grupos em cada agrupamento para determinar o número de K, como apresentado na Figura 4.9. Então, a ideia deste método é gerar diversos agrupamentos com diferentes números de grupos, com o incremento do número de grupos, o erro total tende a diminuir, até que o erro se aproxime de zero, que é quando terá um objeto por grupo.

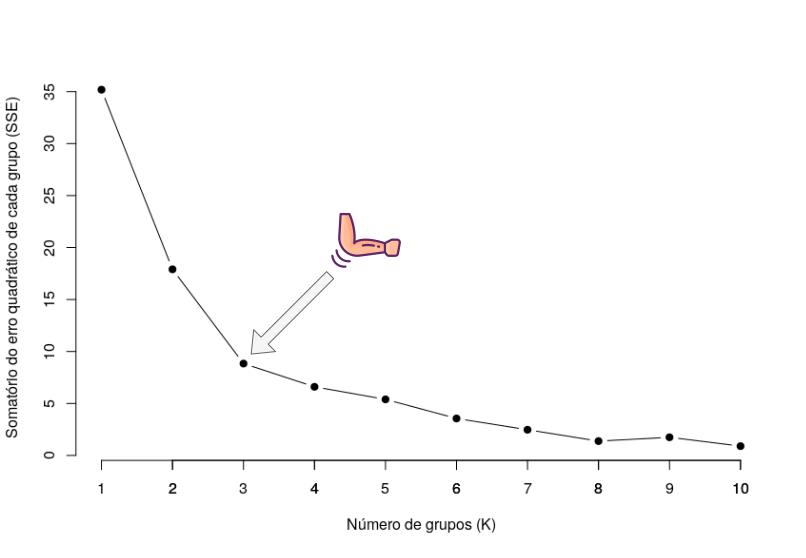
Figure 4.9: Método do cotovelo aplicado no conjunto de dados de exemplo.

De acordo com o método, o número ideal de grupos se dá quando o ponto forma uma curva semelhante de um cotovelo, que é o ponto considerado ideal. Pois os pontos acima do cotovelo estão em uma região de underfitting e abaixo dele em overfitting.

4.3.2.2 Método de Silhueta

O método de Silhueta determina o quão bem cada objeto está alocado em um grupo, ou seja, a homogeneidade de um grupo. O índice de Silhueta varia de -1 a 1. Valores próximos a 1 indicam que o objeto possui semelhança com objetos de seu grupo e dessemelhança com objetos de outros grupos.

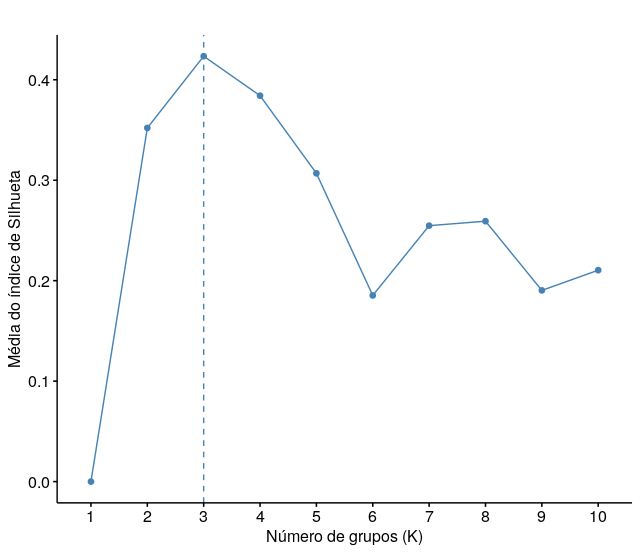
Figure 4.10: Método de Silhueta aplicado no conjunto de dados de exemplo.

A Figura 4.10 mostra um exemplo de aplicação do método de Silhueta, o número ideal de grupos é escolhido com base na maior média do índice de Silhueta, ou seja, neste exemplo apresentado acima, com 3 grupos foi possível obter grupos com objetos semelhantes entre si, e dissemelhante se comparados com objetos de outros grupos.

Agora que entendemos os fundamentos da técnica de agrupamento Kmeans e algumas técnicas de estimativas de grupos, vamos apresentar alguns exemplos práticos na plataforma kaggle, os exemplos estão disponíveis nas linguagens R e Python.

4.4 Agrupamento Hierárquico - Método Aglomerativo

Os métodos de agrupamento hierárquicos que pertencem à categoria de aglomerativos baseiam-se na junção de grupos até que apenas um grupo englobe todos os outros, esse chamado de raiz. No método aglomerativo, os objetos são comparadas com base em uma medida de distância, assim como vimos no Kmeans, em que foi usado a distância euclidiana. No entanto, neste método, os grupos também são comparados, para que a união entre eles seja realizada. Para compararmos a similaridade entre cada grupo usamos as medidas de ligação (do inglês, linkage measures). As medidas de ligação mais conhecidos são:

• Ligação completa ou distância máxima: Em inglês, complete linkage, determina como distância entre dois grupos os pares de objetos mais distantes.

\[dist_{max}(g_1, g_2) = \underset{obj_{g_1} \in g_1,obj_{g_2} \in g_2}{\max \{|obj_1 - obj_2|\}}\]

Em que \(g_1\) e \(g_2\) correspondem aos grupos 1 e 2, respectivamente.

• Ligação única ou distância mínima: Em inglês, single linkage, determina como distância entre dois grupos os pares de objetos mais próximos.

\[dist_{min}(g_1, g_2) = \underset{obj_{g_1} \in g_1,obj_{g_2} \in g_2}{\min \{|obj_1 - obj_2|\}}\]

• Distância baseada em média: Em inglês, average method, determina como distância entre dois grupos a média das distâncias entre os pares objetos.

\[dist_{avg} = \frac{1}{|g_1||g_2|} \sum_{i = 1}^{g_1}\sum_{j=1}^{g_2}dist(obj_i, obj_j)\]

Para exemplificar o funcionamento do método aglomerativo, vamos usar o conjunto de dados apresentado na Figura 4.11, no qual é possível observar 6 objetos (A,B,C,E,F) em um plano cartesiano (X,Y).

Os objetos foram marcados para facilitar a visualização do dendograma.

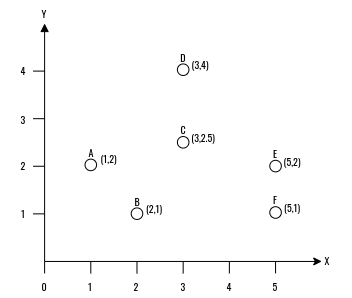
Figure 4.11: Conjunto de dados utilizado como exemplo.

Como foi mencionado, os métodos aglomerativos iniciam de forma em que cada objeto seja seu próprio grupo, e, com isso, a cada iteração os grupos vão se juntando e combinando os objetos dentro deles. O primeiro passo dos algoritmos hierárquicos, abrangendo às duas categorias, divisivos e aglomerativo, é calcular a matriz de distância entre todos os objetos. A Figura 4.12 mostra um exemplo do cálculo da distância do objeto A entre os outros.

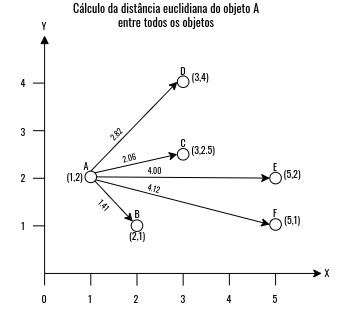
Figure 4.12: Conjunto de dados utilizado como exemplo.

Repare que é necessário calcular as distâncias entre os outros objetos: \(B -> C, B -> D, B -> E, B -> F\); \(C -> D, C -> E, C -> F\); \(D -> E, D -> F\) e \(E -> F\). Vamos deixar como tarefa para que você calcule a distância euclidiana entre os outros objetos.

Então, seguindo com o algoritmo do método aglomerativo, o próximo passo consiste na junção dos objetos em grupos, como foi dito, cada objeto inicialmente pertence ao seu próprio grupo. A etapa de junção dos objetos aos grupos segue a mesma ideia que vimos no Kmeans, só que aqui estamos comparando dois objetos, e não os objetos com seus centróides. Então, os objetos mais próximos se juntam em um grupo, como apresentado na Figura 4.13. A junção segue uma ordem, os objetos com as menores distâncias se juntam primeiro, então, neste exemplo, primeiro vamos juntar os objetos E e F que estão em 1 unidade de distância, depois juntamos os objetos A e B, como mostrado na Figura 4.12, que possuem a distância de \(1.41\), e, por fim, juntamos os objetos D e C que possuem a distância de \(1.5\). Utilizando o Dendrograma é possível observar essas distância no eixo de Altura.

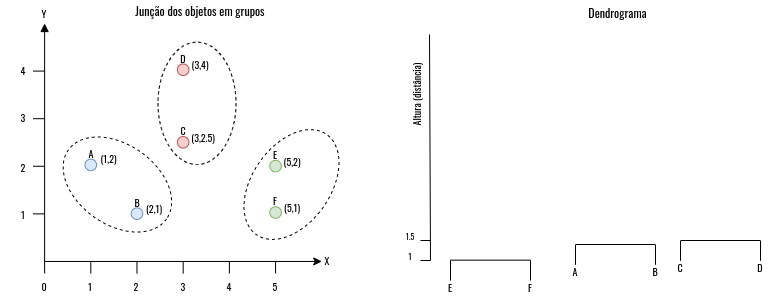
Figure 4.13: Etapa de junção dos objetos.

Depois de juntarmos todos os pares de objetos em um grupo, que até então estavam em seus próprios grupos, é hora de juntarmos os grupos. Nesta etapa de junção dos grupos, vamos utilizar as abordagens de ligação que foram mencionadas acima. A Figura 4.14 apresenta o funcionamento dos métodos de ligação mencionados, em A) temos a ligação completa, que visa juntar os dois grupos mais próximos pelos objetos mais distantes; em B) temos a ligação única, que faz a junção de modo oposto do que vimos em A), usando os objetos mais próximos de cada grupo, e em C) temos a ligação pela média, que visa realizar a junção por meio da média das distâncias entre cada objeto dos dois grupos.

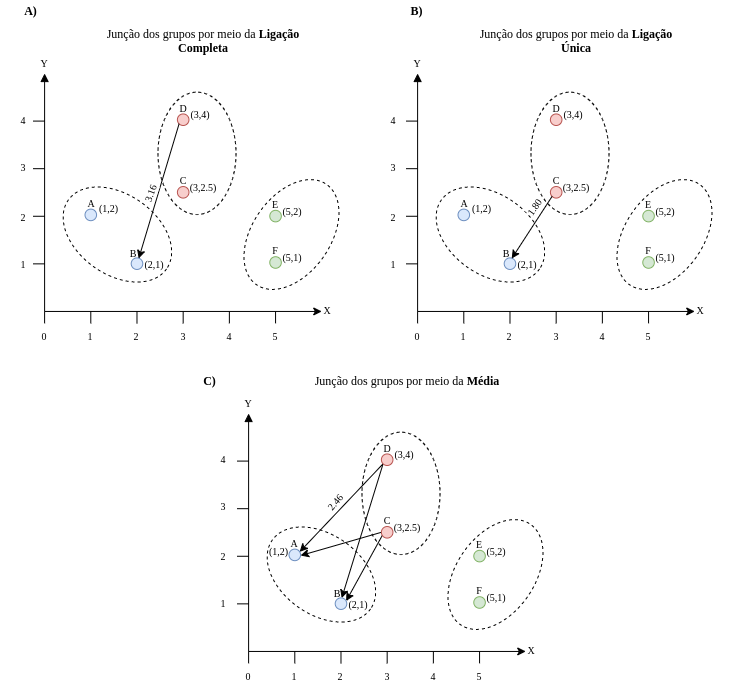
Figure 4.14: Etapa de junção dos grupos.

Por fim, a Figura 4.15 apresenta o resultado final do agrupamento aglomerativo por meio do método de ligação completa, veja que ao final apenas um grupo engloba todo os objetos. Na junção do grupo que engloba os objetos A, B, C e D com o grupo dos objetos E e F, a distância máxima (4.16) se dá pelos objetos A e F.

Vamos deixar como tarefa para que você monte os dendrogramas dos métodos de ligação única e por média. Lembrando que o dendrograma mostra a distância entre os grupos por meio do eixo de altura. Desta forma, o dendrograma varia com o método de ligação. Por exemplo, o dendrograma do método de ligação única é mais achatado, visto que a maior altura corresponde a 2.06.

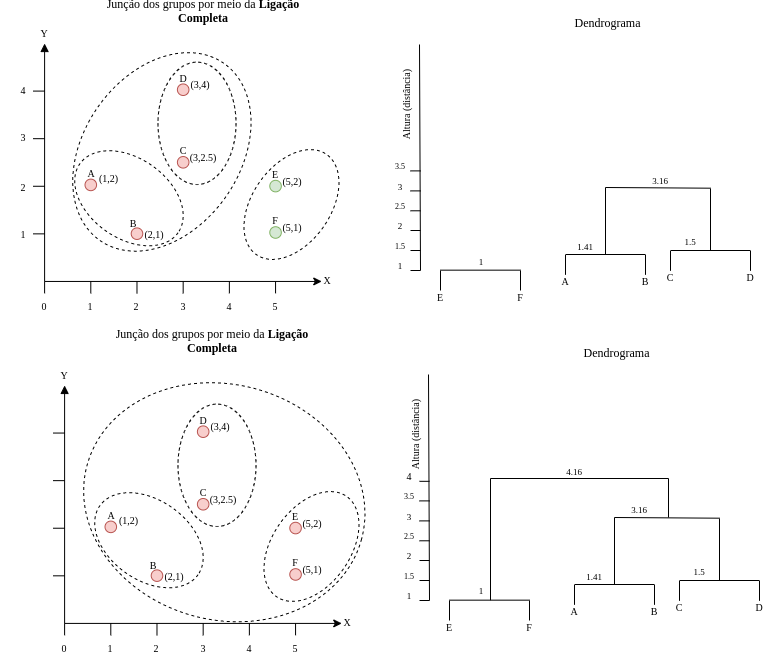
Figure 4.15: Etapa de junção dos grupos - Parte 2.

Resumidamente, podemos descrever o algoritmo do método aglomerativo conforme as etapas abaixo:

• (1º Passo) Crie a matriz de distância entre os objetos;
• (2º Passo) Faça com que cada objeto seja um grupo;
• (3º Passo) Junte os grupos mais próximos;
• (4º Passo) Atualize a matriz de distância;
• (5º Passo) Repita o passo 3 e 4 até que apenas um grupo englobe todos os objetos.

Agora que entendemos como funciona o método aglomerativo, você deve estar se perguntando: “Qual método de ligação devo usar?” e é isso é o que vamos ver agora.

4.4.1 Qual método de ligação deve ser usado?

Assim como a escolha do número de grupos no Kmeans, a escolha do método de ligação também é essencial, no entanto, cabe ao usuário testar os diversos métodos de ligação para determinar qual se adequa melhor ao seu caso. Vamos listar algumas vantagens e desvantagens dos métodos mencionados acima com base do material dos professores Gao and Zhang (2012).

Método	Vantagens	Desvantagens
Ligação única	Consegue lidar com formas não elípticas	Sensível a ruídos e outliers
Ligação Completa	Consegue lidar melhor com ruídos e outliers	Tende a quebrar grandes grupos; Possui viés para agrupamentos com dados circulares.
Distância baseada em média	Consegue lidar melhor com ruídos e outliers	Possui viés para agrupamentos com dados circulares.

Além dos métodos de ligação mencionados acima, existem outros que são igualmentes importantes, como: Ward e Centróide

4.4.2 Como visualizar os grupos no dendrograma?

Como vimos, o dendrograma mostra a hierarquia do nosso agrupamento com o formato de árvores, aos que estão familiarizados com estrutura de dados, uma árvore binária. Assim, podemos fazer um corte nessa árvore e selecionar os grupos que desejamos de acordo com a altura especificada. Por exemplo, a Figura 4.16 mostra a aplicação do método aglomerativo por meio de ligação completa no conjunto de dados utilizado no exemplo do Kmeans, os \(K\)’s em cada dendrograma é o nível em que o corte foi realizado. Desta forma, cortando um nível abaixo da raiz, ou seja, \(k = 2\), obteve-se dois grupos, com \(k = 5\), obteve-se cinco grupos, e assim por diante. O corte no dendrograma nos dá uma visão dos grupos intrínsecos em cada nó da árvore, o que pode auxiliar no entendimento do conjunto de dados

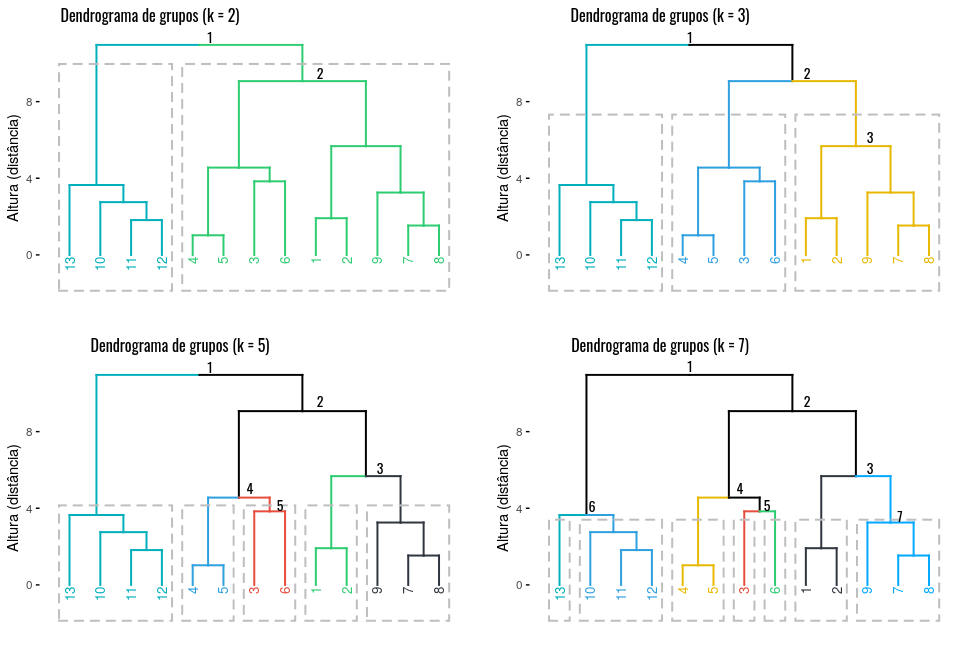
Figure 4.16: Cortes nos dendrogramas para visualização dos grupos.

Como mostrado acima, o \(k\) define a quantidade de grupos que serão mostrados no dendrograma através de um corte feito numa árvore binária. E como foi visto no Kmeans utilizamos as heurísticas do cotovelo e silhueta para determinar o número de \(k\), o que pode ser feito neste método também.

Você deve estar se perguntando: “Como faço para avaliar os grupos gerados no corte?”. Para avaliarmos a qualidade dos grupos podemos usar o índice de Silhueta, que verifica o quão bem os objetos foram ajustados em um grupo e quão eles se diferenciam dos objetos de outros grupos.

Agora que entendemos os fundamentos da técnica de agrupamento aglomerativa e como podemos definir os grupos, vamos apresentar alguns exemplos práticos na plataforma kaggle, os exemplos estão disponíveis nas linguagens R e Python.

Referências Bibliográficas

Aghabozorgi, Saeed, Ali Seyed Shirkhorshidi, and Teh Ying Wah. 2015. “Time-Series Clustering–a Decade Review.” Information Systems 53. Elsevier: 16–38.

Developers, Google. 2020. “Clustering Algorithms.” Google inc.

Esling, Philippe, and Carlos Agon. 2012. “Time-Series Data Mining.” ACM Computing Surveys (CSUR) 45 (1). ACM New York, NY, USA: 1–34.

Gao, Jing, and Aidong Zhang. 2012. “CSE 601: Data Mining and Bioinformatics.” University at Buffalo.

Gasch, Audrey P, and Michael B Eisen. 2002. “Exploring the Conditional Coregulation of Yeast Gene Expression Through Fuzzy K-Means Clustering.” Genome Biology 3 (11). Springer: research0059–1.

Han, Jiawei, Jian Pei, and Micheline Kamber. 2011. Data Mining: Concepts and Techniques. Elsevier.

He, Tao, Yu-Jun Sun, Ji-De Xu, Xue-Jun Wang, and Chang-Ru Hu. 2014. “Enhanced Land Use/Cover Classification Using Support Vector Machines and Fuzzy K-Means Clustering Algorithms.” Journal of Applied Remote Sensing 8 (1). International Society for Optics; Photonics: 083636.

Jain, Anil K. 2010. “Data Clustering: 50 Years Beyond K-Means.” Pattern Recognition Letters 31 (8). Elsevier: 651–66.

Wang, Jiaqi, Xindong Wu, and Chengqi Zhang. 2005. “Support Vector Machines Based on K-Means Clustering for Real-Time Business Intelligence Systems.” International Journal of Business Intelligence and Data Mining 1 (1). Inderscience Publishers: 54–64.