1 Introdução 🗺

A aplicação de dados espaciais no entendimento de um fenômeno geográfico data-se muito antes da criação dos computadores como os conhecemos. Um famoso exemplo no estudo de “análises espaciais de dados” foi pioneiro em relacionar variáveis estudadas a sua localização geográfica. Em meados do século XIX, durante uma das epidemias de cólera na cidade de Londres, John Snow foi bem-sucedido em determinar o epicentro da epidemia. Cruzando a localização das casas em que ocorreram óbitos por cólera com pontos de abastecimentos de água para consumo humano da cidade, John Snow foi capaz de determinar a forma de transmissão da doença e identificar a bomba de água localizada em “broad-street” como crítica (Figura 1.1).

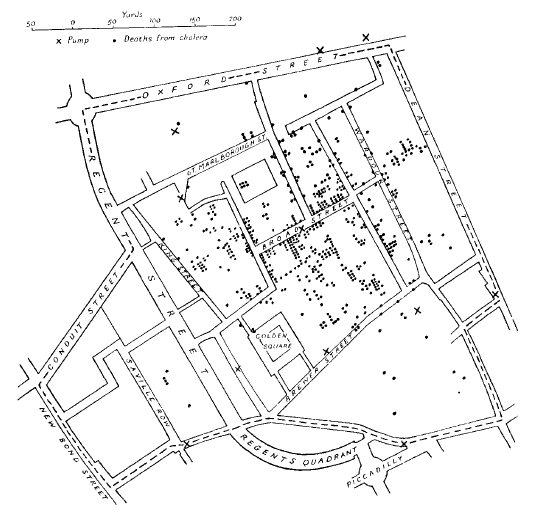
Figure 1.1: Mapa de Londres com óbitos por cólera (pontos) e poços de água (cruzetas)

Como abordado anteriormente, o uso de dados espaciais abrangem diversas aplicações, tais como: estudo de concentração espacial na distribuição de roubos, análise de regiões para fins de zoneamento agrícola e estimativa da extensão de um depósito mineral em uma região a partir de amostras (Monteiro et al. 2004). Desta forma, sempre que onde aparece no problema a ser estudado, usa-se recursos computacionais e ferramentas voltadas para análise de dados espaciais. A Figura 1.2 apresenta alguns equipamentos de coleta de dados espaciais, como satélite, radar e VANT (Veículo aéreo não tripulado).

Figure 1.2: Fontes de dados espaciais - Fonte: (waypoint 2015)

Com o avanço do potencial computacional e subsequente desenvolvimento dos SIG (Sistemas de Informação geográficas) permitiu-se um maior desenvolvimento de estudos voltados à fenômenos geográficos, reduzindo assim custos e facilitando a manipulação de dados espaciais. Ainda que com uma defasagem temporal, no Brasil esta área seguiu em forte desenvolvimento, e apresenta-se hoje aplicada tanto no meio corporativo quanto no meio acadêmico. Em relação às produções acadêmicas podemos citar trabalhos realizados no INPE (Instituto Nacional de Pesquisas espaciais), apresentando qualidade Internacional com publicações em revistas altamente conceituadas. Tomando como exemplo trabalhos desenvolvidos atualmente no curso de pós-graduação em sensoriamento remoto do INPE, podemos visualizar a gama de utilização de dados espaciais para o entendimento dos mais diversos fenômenos. Estes estudos vão desde aplicações em macro escala como o monitoramento da Amazônia brasileira, em função do desmatamento, das queimadas e a deterioração dos recursos hídricos, bem como em escalas mais finas como estudos em reservatórios, áreas urbanas e de luzes noturnas. A Seção Para saber mais apresenta alguns estudos desenvolvidos no INPE.

O objetivo deste minicurso é apresentar de forma simples e objetiva os conceitos fundamentais de dados espaciais, bem como métodos para analisá-los. Sinta-se à vontade para contribuir com este material, esperamos que goste deste pequeno material produzido! 🥼

1.1 Representações de dados espaciais

Dentro do universo estrutural dos SIGs (Sistema de Informação Geográficas), a forma de representação dos dados geográficos podem ser divididas em duas grandes classes: vetoriais e matriciais. Sendo que as estruturas de dados vetoriais são representações que denotam as fronteiras de entidades geográficas, ou seja, através de suas características é possível descrever computacionalmente as formas de uma superfície. Já a classe matricial, representa informações estruturadas em forma de matriz (linhas e colunas). Cada elemento dessa matriz é formado por um determinado valor associado a sua localização e formalmente pode ser representado como uma matriz P(m,n) composto de m colunas e n linhas. Contudo a representação dos dados espaciais é composto por uma gama de grupos pertencentes às representações vetoriais e matriciais, de tal forma que cada grupo deve ser explorado e suas particularidades aprofundadas separadamente.

1.1.1 Vetoriais

A estrutura de dados espaciais no formato vetorial é utilizada para representar a fronteira de uma entidade geográfica, sendo que suas coordenadas espaciais são os pontos que descrevem a posição e direção de um objeto. Para a classe de estruturas vetoriais, suas entidades básicas (Figura 1.3) são representadas nas formas de pontos, linhas e polígonos.

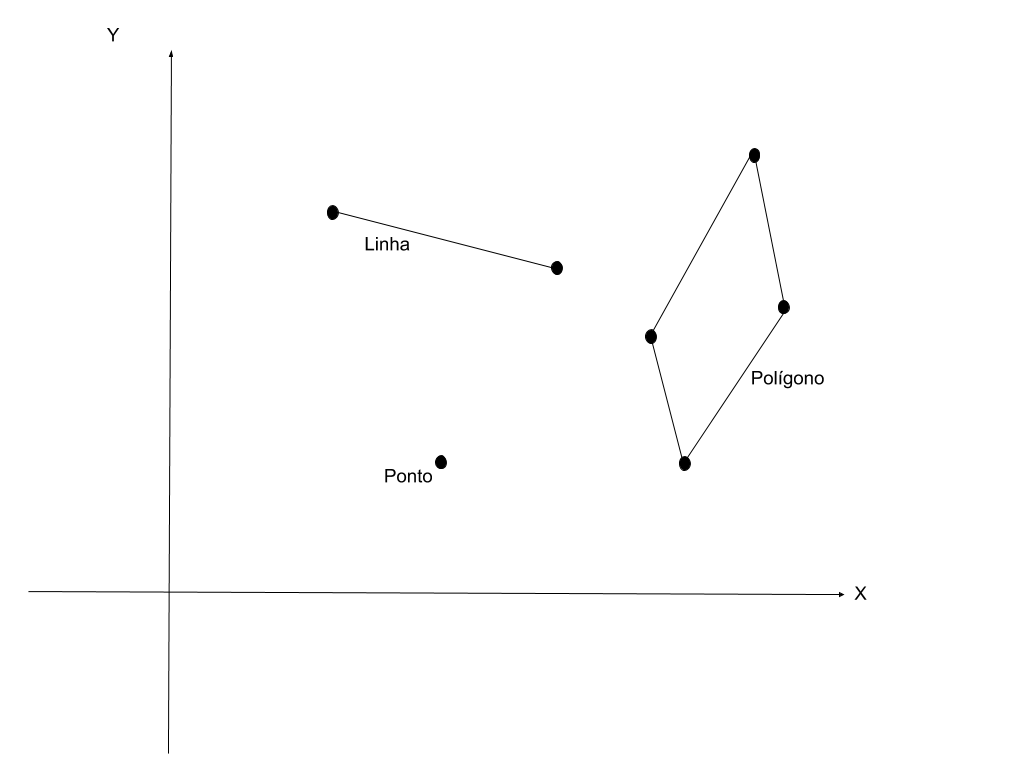
Figure 1.3: Representação no plano unidimensional das formas vetoriais.

Um ponto tem como finalidade a identificação ou localização de uma ocorrência no espaço, onde um par ordenado (x,y) de coordenadas é utilizado para identificar sua posição geográfica, um dos exemplos para representação de pontos pode ser exemplificado como a localização do ponto central de uma cidade ou localidade. Uma linha é composta por um conjunto de pontos e representa uma estrutura unidimensional no espaço, é bastante utilizada para representação de rios e estradas. Um polígono “é a região do plano limitada por uma ou mais linhas poligonais conectadas de tal forma que o último ponto de uma linha seja idêntico ao primeiro da próxima” Casanova et al. (2005).

1.1.2 Matriciais

Diferente das representações vetoriais, onde cada fenômeno é apresentado como um objeto espacial, nas estruturas matriciais (raster) os atributos presentes nos fenômenos estão associados a elementos em uma matriz. Cada valor armazenado na estrutura matricial têm suas características relacionadas a uma posição, essa posição também é chamada de célula, e é responsável por armazenar um valores que representam uma área específica da superfície.

Uma das características presentes nas estruturas matriciais é a resolução espacial que corresponde a um valor relacionado a dimensionalidade linear em um espaço geográfico. “Quanto menor a dimensão das células, maior a resolução da imagem matricial e, consequente, maior a quantidade de memória necessária para armazená-la” Lisboa Filho and IOCHPE (2001).

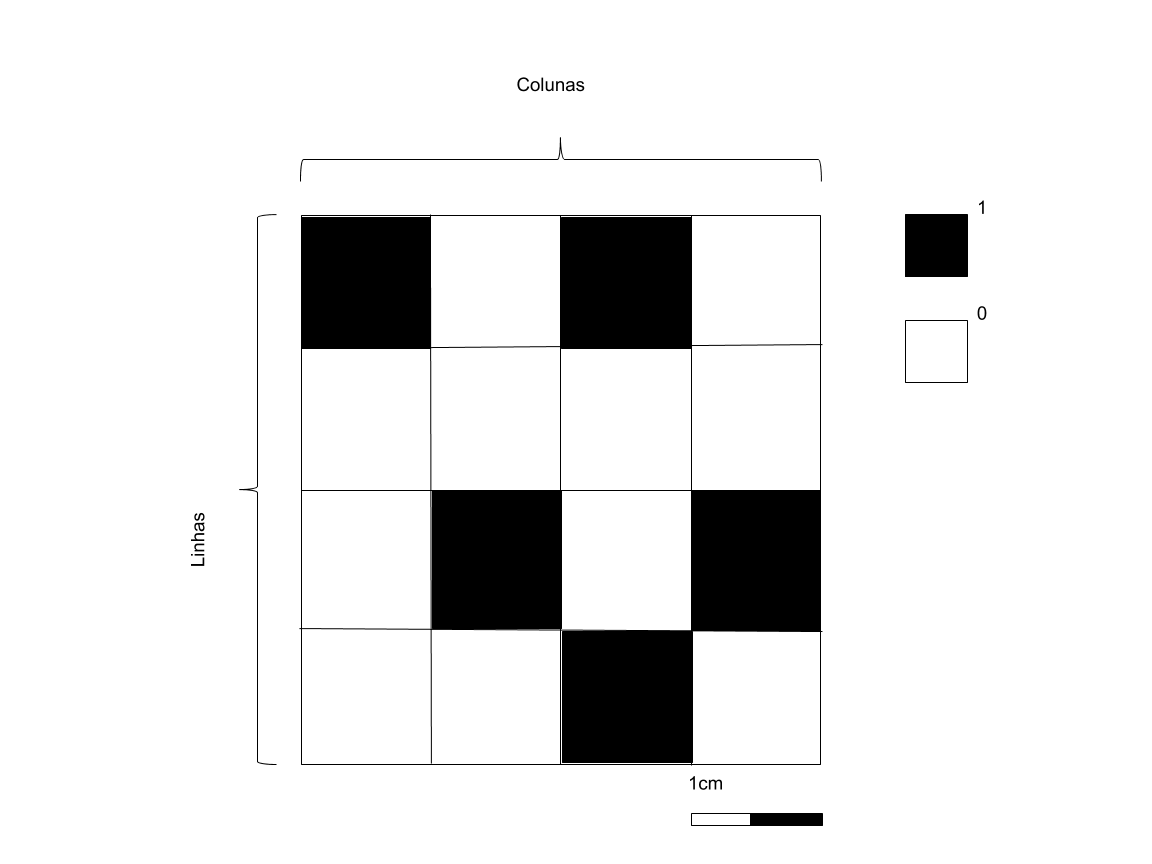
Figure 1.4: Estrutura para representação matricial onde cada célula tem um valor de atributo (UM ou ZERO)

A representação matricial pressupõe que o espaço amostral dos elementos que compõem uma superfície plana tenham um valor de atributo associado, ou seja, cada célula está contém um valor e uma localização (linha e coluna) da matriz. Além da representação simples, é possível generalizar que os espaços celulares podem estar associados a mais de um atributo, ou seja, uma quantidade maior de fenômenos está associada a uma localização da matriz, essa associação pode ser do tipo espaço-temporal para retratar fenômenos dentro de uma série temporal, esta forma de representação é muito conveniente para armazenar os dados no formato de bancos de dados do tipo objeto-relação.

1.2 Sistema de referência espacial

Bem, como vimos até aqui, dados espaciais possuem duas características fundamentais, o registro de diferentes fenômenos e sua localização. Mas como esta localização é vinculada a uma posição da superfície terrestre?

Para conseguirmos responder a esta pergunta devemos ir por partes. Vamos começar imaginando uma superfície plana, como a apresentada abaixo.

Agora perceba que, para gerar tal superfície o que precisou ser feito foi delimitar quatro pontos e então ligar cada um deles, veja.

Até aqui apenas criamos uma superfície e delimitamos seu espaço através dos pontos ABCD, vamos agora inserir valores para os lados desta superfície.

Lembre-se que, está superfície representa um quadrado, e assim, todos os seus lados têm o mesmo tamanho.

Certo! Com os limites definidos podemos agora adicionar um ponto nesta superfície, isto porque, se cada um dos lados vai de 0 a 10, conseguimos facilmente inserir um ponto utilizando os lados como referência.

Ok, mas, o que é isso tem a ver com sistemas de referência espacial e nossa pergunta inicial? Tudo! Isto já que, para sabermos onde estava o ponto e sua localização precisamos definir os limites da superfície, e a mesma situação é necessária para os dados espaciais e a superfície terrestre.

Então, com a mesma lógica aplicada à superfície quadrada do exemplo anterior podemos mapear todo o planeta Terra, porém alguns problemas surgem para este caso. Primeiro, para começarmos a mapear a superfície terrestre devemos entender:

• Como é a superfície terrestre; e
• formas de representação.

Começando com a superfície terrestre, as ciências geodésicas, que se empenham em realizar os estudos das formas e dimensões da Terra dividem sua superfície em três formas diferentes (Montanari 2014).

Na Figura acima o geóide representa tudo que está no nível do mar, o elipsóide representa a camada abaixo do geóide e o terreno a parte superior ao geóide, além disto, tanto a representação da superfície terrestre quanto o geóide carregam diversas dificuldades quando precisam ser representados, por conta de suas características irregulares, por isso, adota-se como representação da superfície, o elipsóide

Com isto, pode-se concluir que, o geóide é a superfície de medição da Terra, enquanto o elipsóide é a superfície de representação.

Certo, com a definição da forma de representação da superfície terrestre já podemos realizar todo o mapeamento, correto? Ainda não, pois além de entendermos como é a superfície precisamos definir como toda esta superfície terrestre será representada. Tal representação pode ser feita de diversas formas, a variar de acordo com a necessidade, algumas dessas formas são apresentadas na Figura abaixo.

Onde, a superfície esférica normalmente é utilizada como representação da Terra quando há grandes quantidades de área a serem representadas, como por exemplo, diversos continentes ou mesmo o planeta todo (Montanari 2014) . Já para os casos, onde é necessário a representação de uma quantidade de Terra considerável, porém, não tão grande como o planeta todo, utiliza-se a representação elipsóidica (Montanari 2014), esta que inclusive é a mais utilizada nas aplicações espaciais atuais. Por fim, tem-se o modelo geoidal, que como já citado, é o que mais se aproxima da superfície terrestre, porém sua representação pode ser muito complexa para o mapeamento da superfície terrestre e a geração das localizações.

Beleza! Agora entendemos todo o fluxo necessário para realizar do mapeamento, partindo da definição da superfície e indo até suas formas de representação. Com isto, conseguimos fazer uma definição de sistemas de referência espacial que seja clara e concisa.

Sistemas de referência espacial, ou DATUM, é um sistema coordenado, utilizado para representar características físicas e geométricas do planeta Terra.

Alguns exemplos de sistemas de referência espacial são:

• WGS 84;
• Sirgas 2000.

Muito interessante, porém, mesmo com este entendimento ficou uma dúvida, como é que os pontos vão ser representados, da mesma forma que havíamos feito no exemplo? Bem, esta pergunta é respondida nas seções seguintes.

1.3 Projeções cartográficas

Até esta seção, todas as informações passadas de representações da superfície terrestre utilizaram modelos tridimensionais para tal feito, porém, se estas representações possuem três dimensões, como mapas bidimensionais, com o apresentado abaixo são gerados?

A resposta é simples! Projeções cartográficas, estas que através de transformações geométricas realizam a conversão das representações tridimensionais para bidimensionais, mantendo a correspondência entre ambas IBGE (2016a).

1.3.1 Tipos de projeção

Por se tratar de operações geométricas é esperado que nessas existam distorções (IBGE 2016a), por conta disto existem diferentes tipos de superfícies geométricas de projeção que são utilizadas (IBGE 2016b), para que as superfícies no momento da projeção foram a menor quantidade possível de distorções nas áreas de interesse.

As subseções a seguir apresentam alguns tipos de superfícies geométricas utilizadas para as projeções.

1.3.1.1 Projeção cilíndrica

Na projeção cilíndrica o esferóide de representação da Terra é envolvido sobre um cilindro tangente.

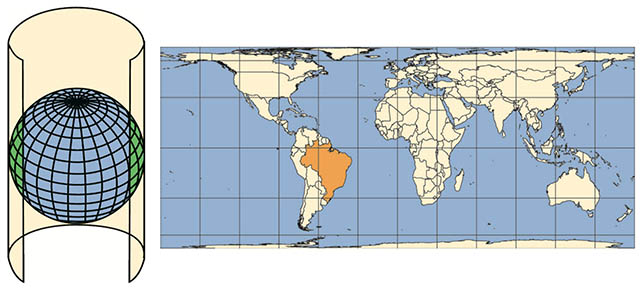
Neste tipo de projeção há muitas distorções dos polos, sul e norte, o que faz com que estes pareçam ter tamanhos bem maiores do que deveriam.

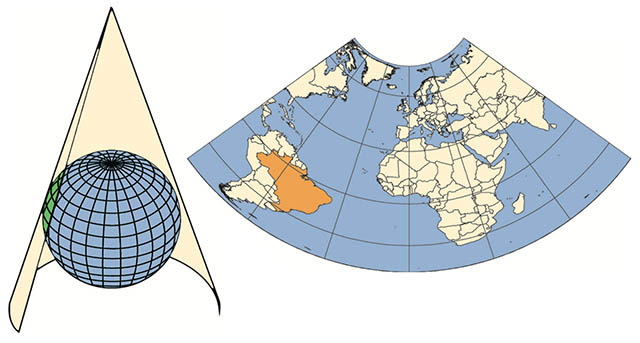
1.3.1.2 Projeção Cônica

As projeções cônicas são geradas através da utilização de um cone, que favorece a redução de distorções nos meridianos e aumenta a distorção nos polos.

1.3.1.3 Projeção plana

Projeção que é gerada com base em um plano, que toca em um ponto específico da representação da esfera terrestre.

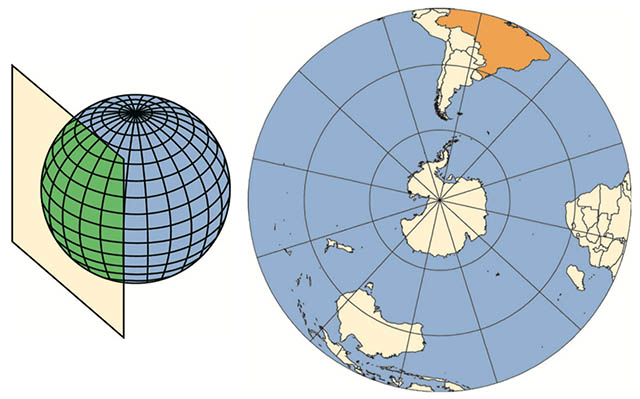
Como é possível perceber na Figura acima, neste tipo de projeção é esperado que haja muitas distorções no entorno do ponto utilizado como referência para sua criação.

1.4 Sistema de Coordenadas

Bem, mesmo com as várias formas de representação e projeção, é mais que necessário utilizamos de alguma técnica que nos permita, dentro de cada uma das representações, apontar sem nenhum tipo de ambiguidade as posições nas quais diferentes objetos estão na superfície terrestre.

1.4.1 Sistemas de Coordenadas Geográficas

Então, para que cada objeto na superfície da Terra fosse facilmente identificado, sem nenhum tipo de ambiguidade, um sistema de linhas imaginárias, nomeado de Sistemas de Coordenadas Geográficas foi criado. Neste sistema existem dois tipos de linhas, os meridianos e os paralelos. Para os meridianos tem-se que são linhas imaginárias que cortam a Terra no sentido norte-sul e para os paralelos, tem-se linhas que circulam a Terra no sentido leste-oeste (IBGE 2016b).

Vale acrescentar também que, os paralelos nos representam as latitudes, que são a distância em graus da linha do Equador até um determinado paralelo. Os valores da latitude podem variar de 0° (Sob a linha do Equador) a 90° (Sob as extremidades), sendo que, para os hemisférios norte são considerados valores positivos e para o hemisfério sul valores negativos. Já as longitudes representam a distância, em graus, entre o meridiano de Greenwich até um outro meridiano qualquer. Seus valores variam de 0° (Sob o meridiano de Greenwich) a 180° (Nas extremidades leste e oeste a Greenwich), onde, para o leste consideram-se valores positivos e ao oeste valores negativos (IBGE 2016b).

A representação de todo este sistema imaginário de linhas pode ser visto na Figura abaixo.

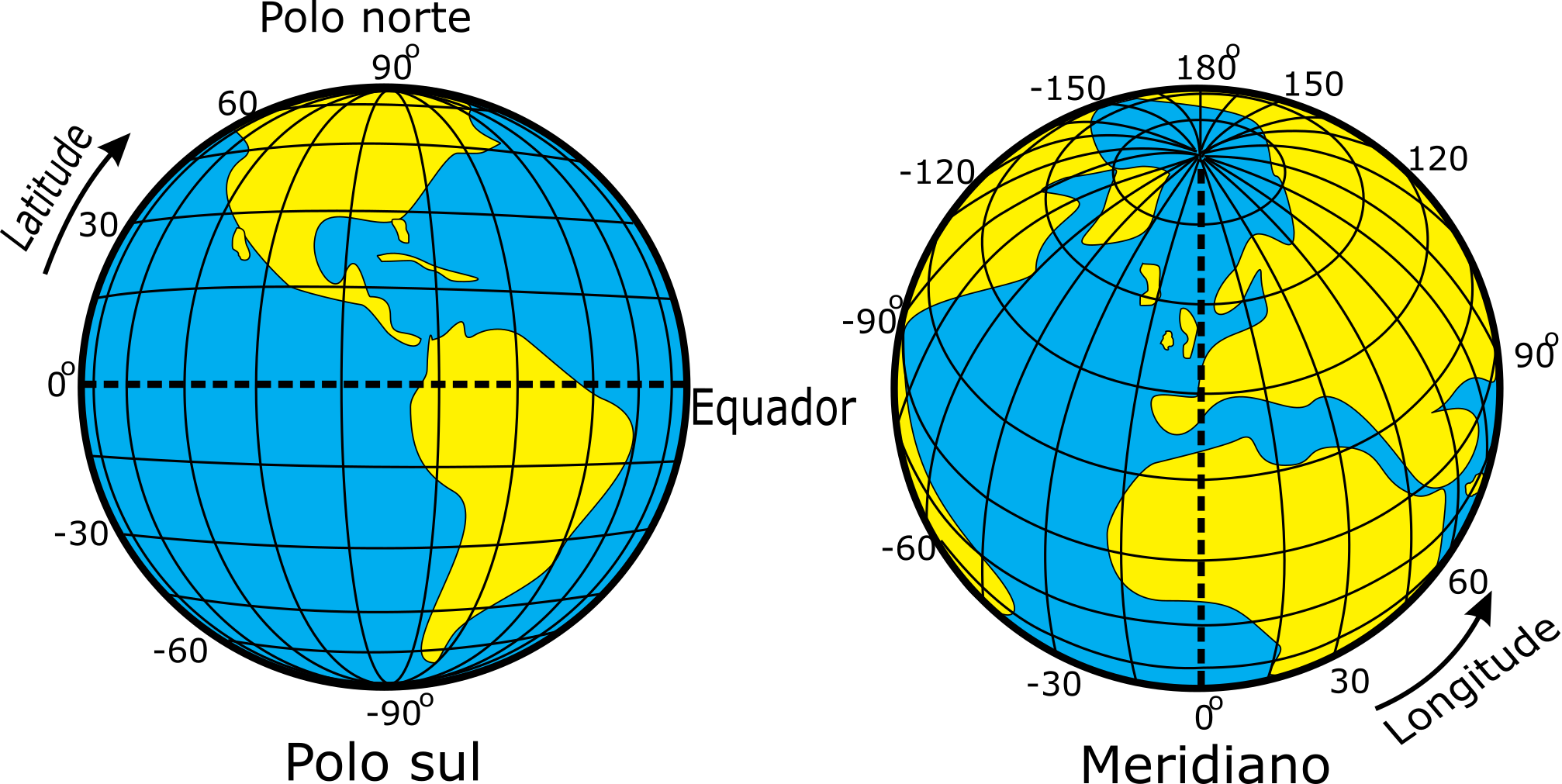
1.4.2 Coordenadas planas

Outra forma de realizar o mapeamento das posições das representações das superfícies terrestres é feita com o método nomeado de Coordenadas planas, que de acordo com Santos, Barbosa, and Gomes (2016) são recomendados para atividades de medições de áreas e distâncias.

O sistema de coordenadas planas é baseado no sistema cartesiano de representação, onde em um plano bidimensional o cruzamento de duas linhas faz a representação da localização de um ponto (Santos, Barbosa, and Gomes 2016), sendo que o eixo X representa a Latitude e o eixo Y a longitude.

Espere um pouco, representação em um plano? Até aqui vimos a representação geográfica que é feita sobre a representação esferoidal da superfície terrestre e só vimos a superfície plana nas projeções. Pois bem, para a utilização do sistema de coordenadas planas é assumido que alguma projeção seja aplicada, normalmente utiliza-se a superfície cônica na projeção dos dados para a utilização deste sistema (Santos, Barbosa, and Gomes 2016).

Lembra do mercator que citamos anteriormente, a forma de representação para coordenadas planas comumente utilizada também é dele, e possui o nome de Sistema Universal Transversa de Mercator.

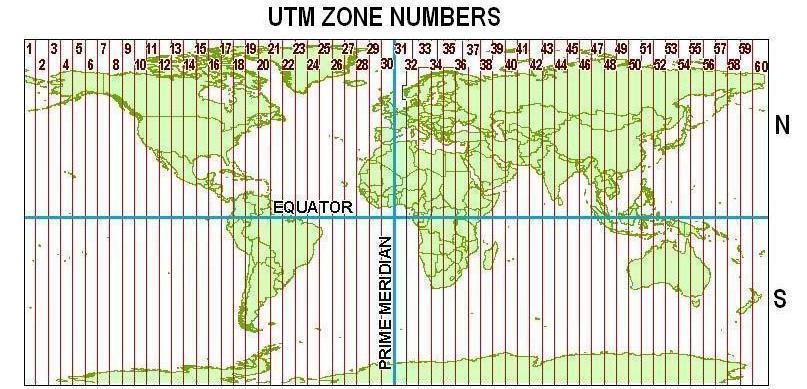
1.4.3 Códigos EPSG

Os códigos European Petrolem Survey Group (EPSG) representam uma forma de organização dos mais diversos sistemas de referências e seus sistemas de coordenadas, desta forma os códigos EPSG criam uma forma rápida e simples para a busca e identificação de qual sistema de referência e sistema de coordenadas está sendo utilizado.

Como estes códigos abrangem todos os sistemas de coordenadas do mundo, com os mais variados sistemas de coordenadas, abaixo é apresentado uma tabela com somente alguns dos códigos EPSG mais utilizados no Brasil.

CÓDIGO EPSG	PROJEÇÃO/DATUM
4225	GCS
4618	Corrego Alegre
4674	GCS SAD69
4326	GCS SIRGAS
22521	2000
22522	GCS WGS84
22523	Corrego

1.5 Open Geospatial Consortium (OGC)

A organização Open Geospatial Consortium (Consórcio Geoespacial Aberto, OGC) é responsável por reunir organizações voluntárias que trabalham no desenvolvimento e implementação de padrões geométricos para o processamento de dados em um SIG. O OGC propõem dentro de suas normas que para dados espaciais existem dois tipos a serem descritos na sua forma simples, geometry (geometria) e geography (geografia) que oferecem suporte a outros dezesseis objetos (ou instâncias) derivados, porém apenas onze podem ser instanciados diretamente. Os modelos de objetos geométricos do OGC possuem características que podem ser descritas dentro do seu conjunto de normas e implementações, essas características fazem parte da arquitetura que descreve objetos comuns chamado Simple Features, aqui chamado de OGC-SFS. Para descrever a hierarquia geometry onde os tipos de dados são baseados, é possível criar instâncias que representam os tipos de dados geográficos, para isso a figura ilustra os principais tipos de dados para geometry e geography.

Figure 1.5: Principais tipos geométricos (OGC) - Fonte: (Egenhofer and Franzosa 1991)

Os tipos de dados espaciais dentro do OGC Simple Features (Figura 1.5) estão divididos em dezesseis tipos de diferentes instâncias, podendo ser divididos em outros três grupos: Primitivos, Múltiplos e Coleções. No tipo primitivo temos os seguintes objetos:

• Ponto (POINT): Um ponto é um objeto 0-dimensional que representa uma localização simples para coordenadas espaciais, sendo composto por um par ordenado de coordenadas (x,y) associados a um sistema de referências espaciais.

• Linha (LINESTRING): É composto por um conjunto de pontos interpolados linearmente onde cada par consecutivo de pontos define um segmento de linha, ou seja um LINESTRING é exatamente a interpolação entre dois pontos ou um conjunto de pontos.

• Polígono (POLYGON): O polígono é definido como uma superfície planar com fronteira exterior e zero ou mais superfícies interiores. Para compor um polígono é necessário que um conjunto de 3 ou mais pontos distintos para formar os vértices do mesmo.

Já para o grupo dos Múltiplos, os tipos de dados relacionados são baseados na coleção dos tipos simples, ou seja, para um MULTIPOINT basta que um conjunto de pontos esteja associado com zero o mais instâncias; Já para MULTILINESTRING o mesmo é aplicado, sendo que o conceito de MULTICURVE múltiplas curvas entre pontos é o que define a coleção de objetos associados, além disso o MultiLineString pode ser do tipo simples, fechada ou não fechada; Já o MULTIPOLYGON pode ser definido como parte de uma superfície bi-dimensional dentro do GeomCollection, onde os elementos são formados por um conjunto de polígonos adjacentes.

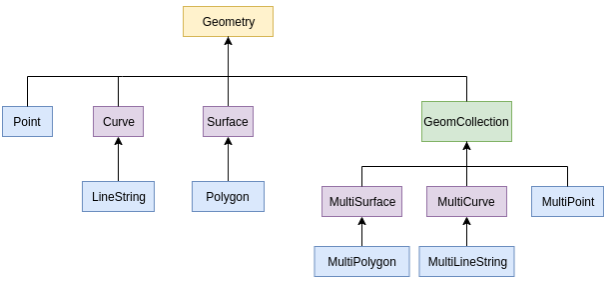
Figure 1.6: Hierarquia da OGC Simple Feature simplificada

Existe uma diferença significativa para os tipos de dados de geometry e geography, os dois se comportam de maneira semelhante porém algumas diferenças importantes devem ser levadas em consideração. Existem tipos de medidas para dados espaciais, dentre estes tipos de medidas podemos destacar as medidas de sistema planar (terra plana) e os sistemas elipsoidal (terra redonda), onde as medidas de distância e áreas possuem variações que devem ser levadas em consideração para obtenção de medidas mais precisas. Assim como as medidas para os dados espaciais é importante determinar a orientação dos dados espaciais, em sistemas planares a orientação do anel do polígono não é um fator importante, já para sistemas elipsoidais um polígono pode ter valores ambíguos caso a sua orientação não seja definida.

1.6 Relacionamentos espaciais

Além da definição dos tipos geométricos, o OGC-SFS define também operações para a manipulação e uso desses. Dentre as operações definidas existem um conjunto delas que merece uma atenção especial, os operadores topológicos, com esses é possível realizar testes de relacionamento espacial entre os objetos geométricos. Na especificação da OGC-SFS, esses operadores topológicos utilizam como base a matriz de 9 intersecções estendida dimensionalmente.

1.6.1 Matriz de 9-Interseções Estendida dimensionalmente

A matriz de nove intersecções extendida dimensionalmente (DE-9IM) tem como objetivo apresentar um método para os relacionamentos topológicos entre objetos geométricos, este modelo considera o resultado da interseção entre as fronteiras, interiores e exteriores de duas geometrias (QUEIROZ and CÂMARA 2005). A matriz é apresentada abaixo

	Interior(B)	Fronteira(B)	Exterior(B)
Interior(A)	\(I(A) \cap I(B)\)	\(I(A) \cap F(B)\)	\(I(A) \cap E(B)\)
Fronteira(A)	\(F(A) \cap I(B)\)	\(F(A) \cap F(B)\)	\(F(A) \cap E(B)\)
Exterior(A)	\(E(A) \cap I(B)\)	\(E(A) \cap F(B)\)	\(E(A) \cap E(B)\)

Com base nestes testes de intersecção faz-se a construção dos operadores de relacionamento especificados na OGC-SFS.

1.6.2 Relacionamentos espaciais nomeados

Com base na sobrecarga de comportamentos específicos da DE-9IM, a OGC-SFS define um conjunto de 8 operadores com nomes bem definidos, de modo que, o comportamento gerado por esses sob a DE-9IM já tem um padrão determinado, o que evita ter de trabalhar diretamente com a manipulação da matriz.

Os operadores definidos são:

\(Equals(Geometry, Geometry) \to bool\): Verifica se duas geometrias são espacialmente iguais

\(Disjoint(Geometry, Geometry) \to bool\): Verifica se duas geometrias não possuem qualquer tipo de relação espacial

\(Touches(Geometry, Geometry) \to bool\): Indica se duas geometrias se tocam

\(Crosses(Geometry, Geometry) \to bool\): Verifica se duas geometrias se cruzam

\(Within(Geometry, Geometry) \to bool\): Verifica se a primeira geometria está dentro da segunda

\(Contains(Geometry, Geometry) \to bool\): Este operador é o inverso do Within, verificando se a primeira geometria contém a segunda

\(Overlaps(Geometry, Geometry) \to bool\): Verifica se duas geometrias se sobrepõem

\(Intersects(Geometry, Geometry) \to bool\): Verifica se duas geometrias tem algum tipo de relacionamento espacial

Com a utilização desses operadores bem definidos, muitas operações em Sistemas de Informação Geográficas são realizadas. Há muito mais para ver, aqui apenas apresentamos os conceitos gerais, para que você tenha uma ideia de tudo que está por trás das operações que são realizadas no curso. Se quiser se aprofundar, o material da disciplina de Bancos de Dados Geográficos é aberto e cobre por completo cada um desses assuntos.